CS224W 2. Traditional Methods for ML on Graphs

1. 机器学习任务

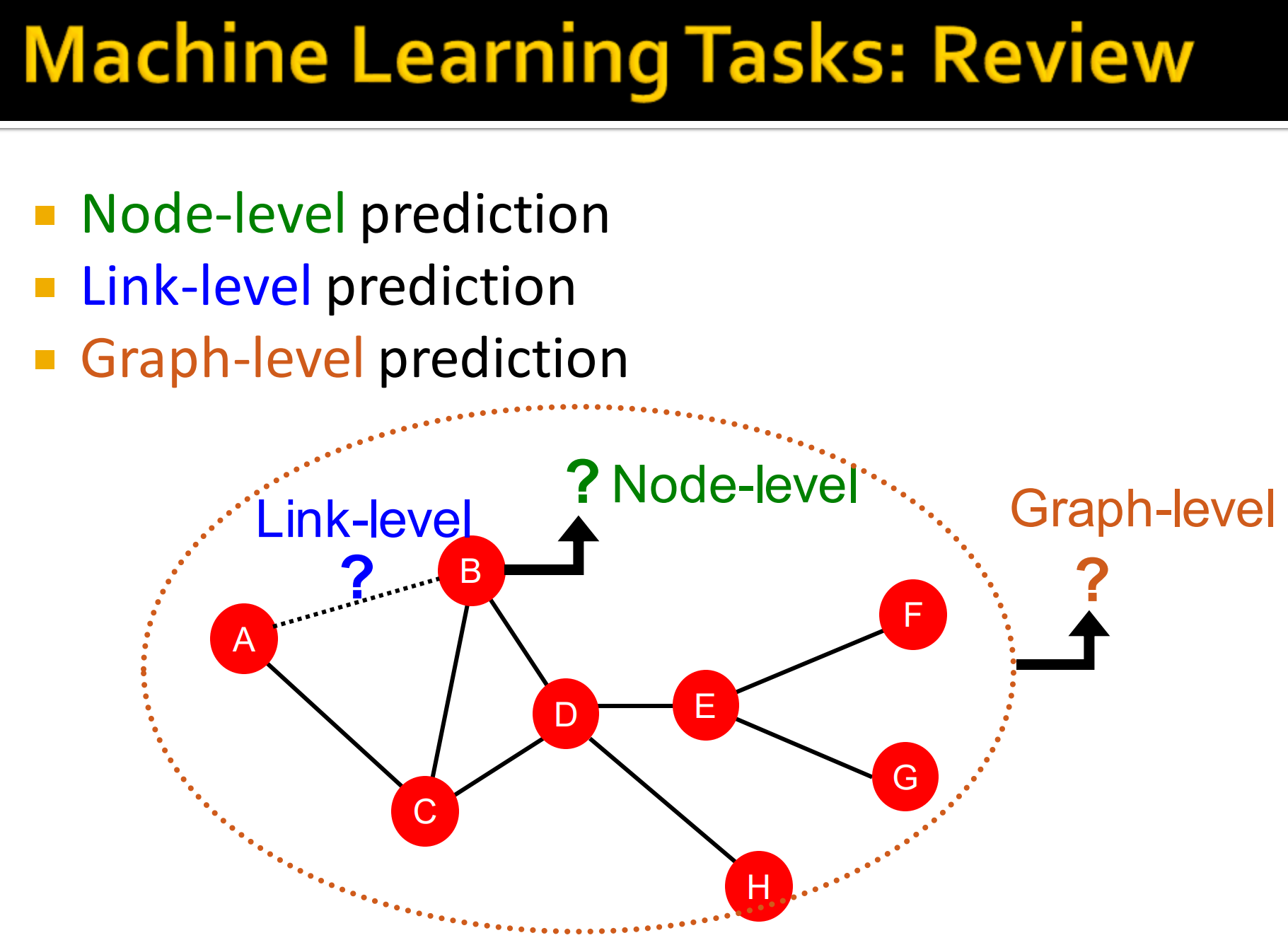
传统机器学习在图网络中的任务分为:

节点级别预测
边级别预测
图级别预测

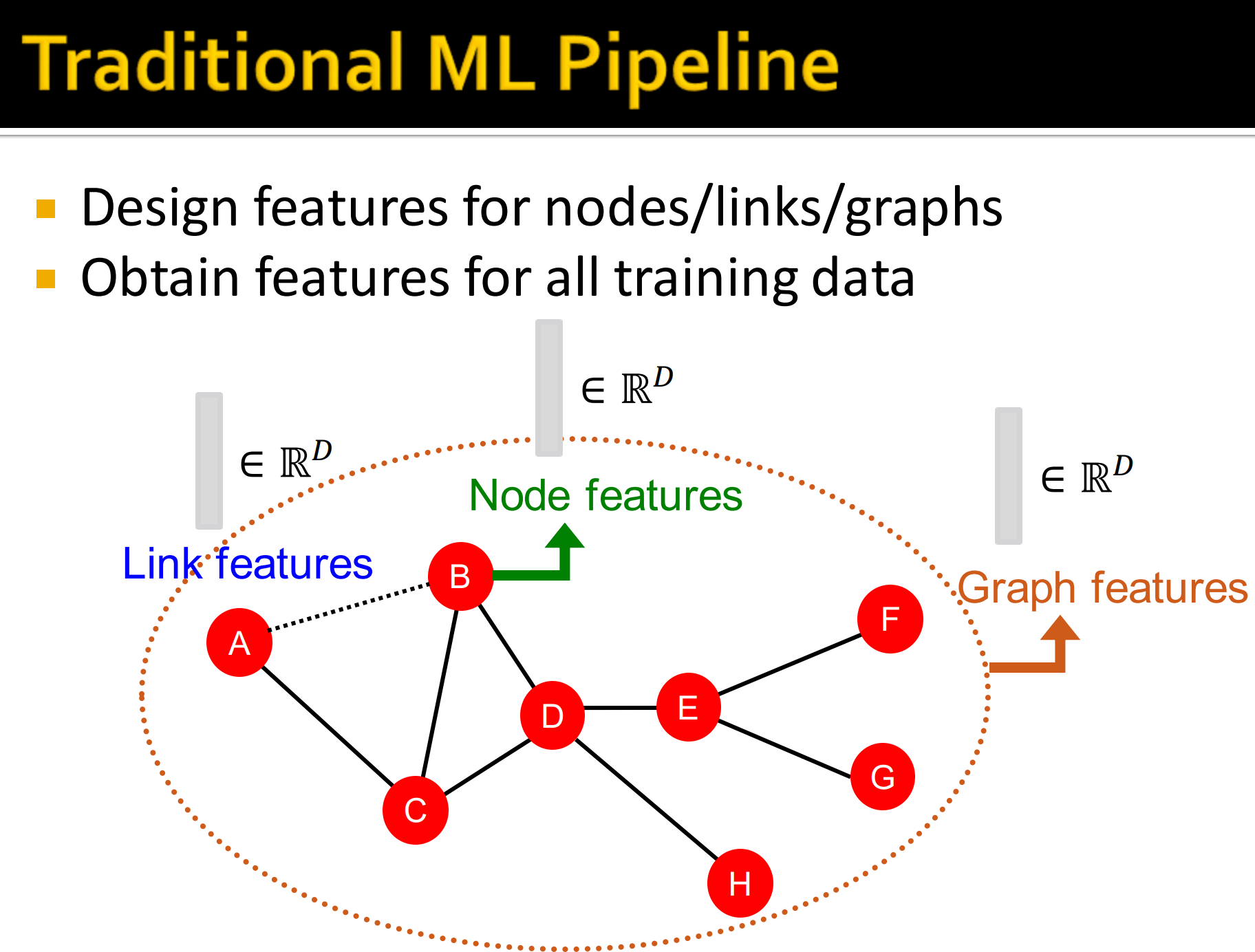
传统机器学习中的Pipeline:

设计节点/边/图相应特征
从训练数据中获取特征

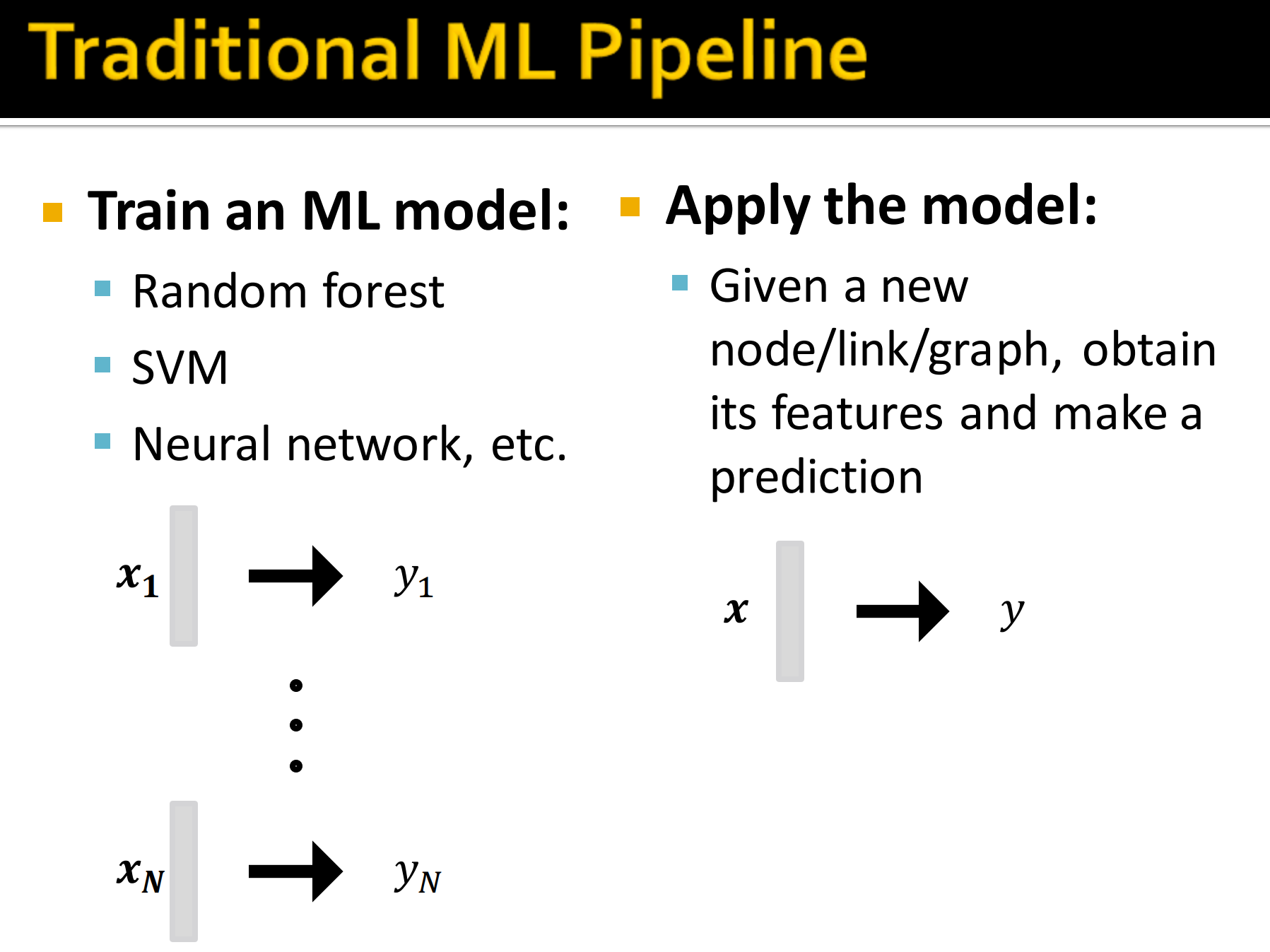
具体来说，就是用：

随机森林
SVM
NN等等

模型在给定新的节点/边/图的情况下用获得的特征来做预测。

在图上使用有效特征是模型取得好的表现的关键。传统ML pipeline使用手工设计的特征。本节，我们会回顾传统特征用来:

节点级别预测
边级别预测
图级别预测

简单来说，本节聚焦于无向图。

2. 图机器学习

目标是:对一系列对象做预测。

设计方案:

特征: d维的向量
对象: 节点、边、一系列节点、整张图
对象函数: 我们要解决什么任务?

例如，节点级别预测，

给定 $G = (V, E)$
学习一个函数 $f: V \to \mathbb{R}$

这样我们的问题就是怎样学到这个函数了,接下来会逐步阐述这个问题。

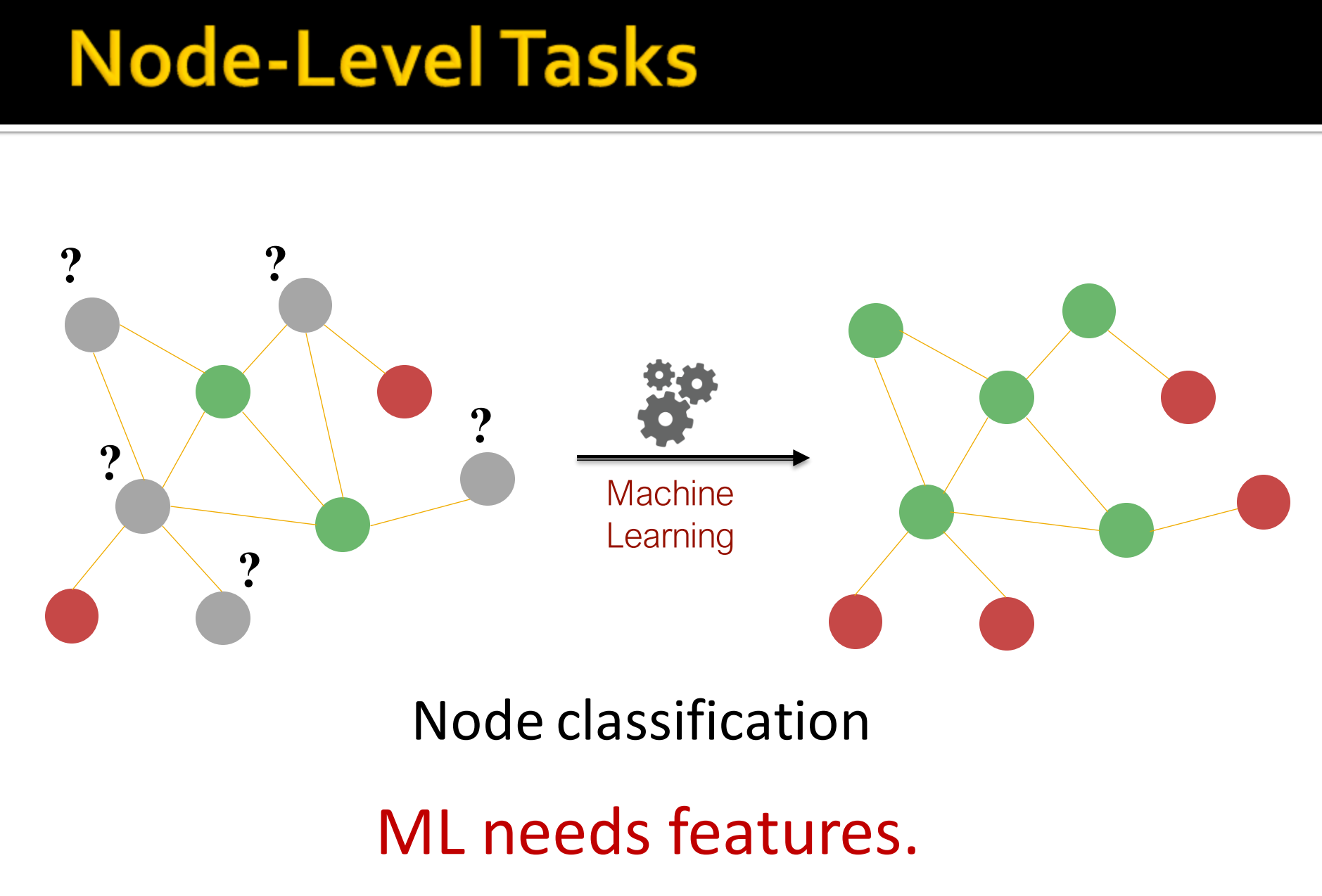
例如上面例子中，绿色的度为2，红色为1，那么我们就可以拿节点的度来做分类，这就是一个节点分类任务。这样我们可以看出机器学习需要特征。接下来我们看看到底有哪些节点特征?

3.节点级别特征概述

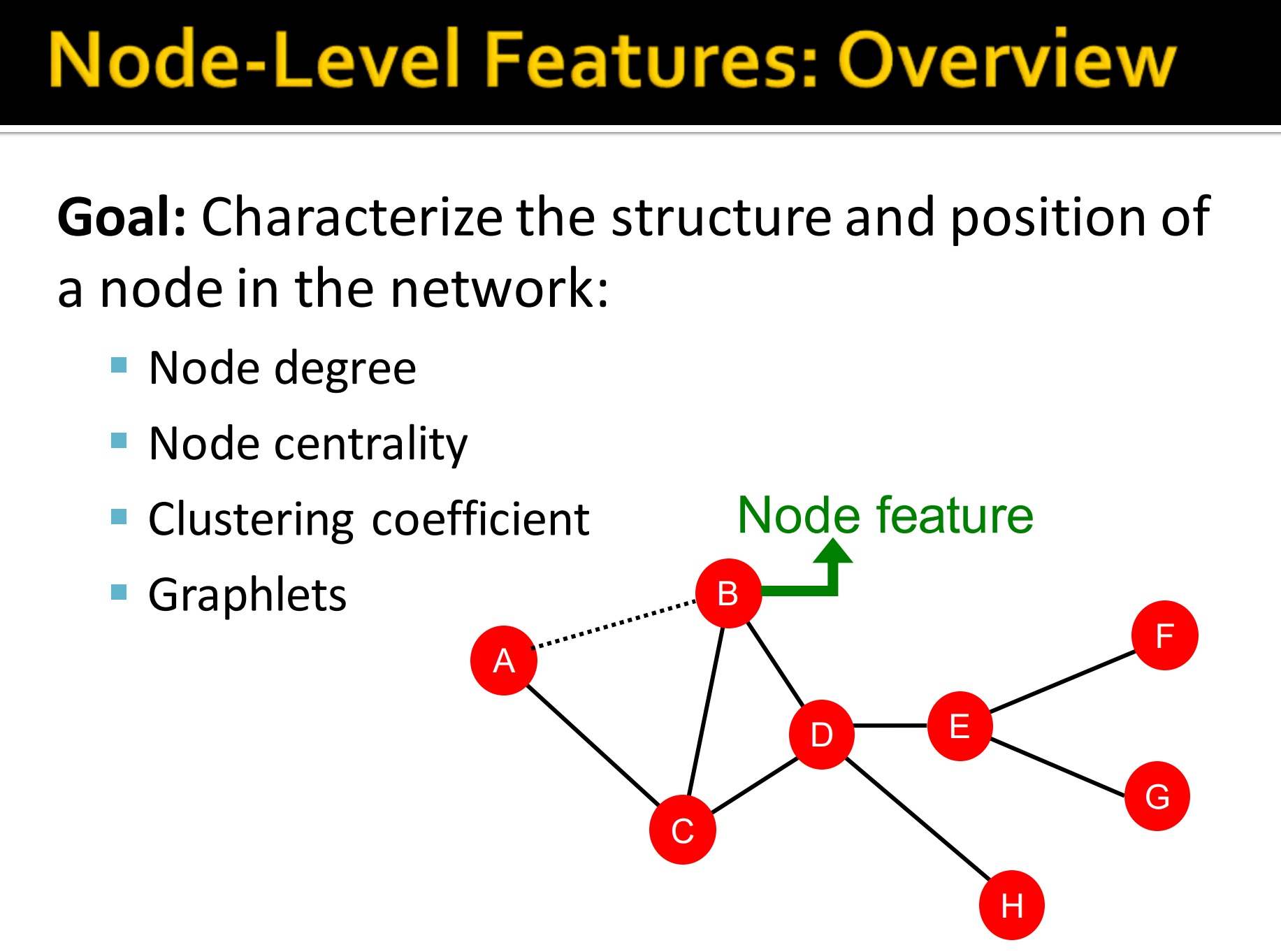
目标:特征化结构与节点在网络中的位置,

节点的度
节点的中心性
聚类系数
graphlets，不同构子图。

1. 节点特征: 节点中心性 centrality

节点度不能衡量邻近节点的重要性。
节点中心性 $c_v$ ：考虑节点在图中的重要性。

例如，A微博粉丝100个，B微博粉丝30个，但B微博粉丝有10个大V，A微博没有。我们考虑节点重要性，在微博粉丝关系图谱中，B节点要重要些。

建模重要性的不同衡量指标:

特征值中心性 Eigenvector centrality
中介中心性 Betweenness centrality
接近中心性 Closeness centrality

注: Social and Economical Networks 中第二章Centrality部分更详细地介绍了中心性。

2. 特征值中心性 Eigenvector centrality

Eigenvector centrality :

节点 $v$ 的中心性由其周围的邻近节点 $u$ 的重要性决定 $u \in N(v)$ 。
对节点 $v$ 的中心性，就是对周围邻近节点的中心性求和，即

式1是用递归的方法构建公式对中心性衡量。那么怎么求解呢?

注: $\lambda$ 是归一化因子。

改写式1易得:

其中：
- $A$ 是邻接矩阵, 表示节点之间的邻居关系
- $\mathbf{c}$ 是中心性向量
- $\lambda$ 是特征值
式2表明中心性 $\mathbf{c}$ 就是 $\mathbf{A}$ 的特征向量，特征值最大 $\lambda_{max}$ 总是正的并且唯一，最大的特征向量 $\mathbf{c}_{max}$ 对应最大的特征值 $\lambda_{max}$ ，这个 $\lambda$ 作为特征中心性来使用。

若一个 $n \times n$ 的矩阵各个元素非负，那它有一个非负特征值 $\lambda$ 严格大于其他所有特征值，其对应的特征向量也非负。特别的，如果该矩阵是不可约的，那么有 $\lambda$ 的重数(multiplicity)为1，且对应特征向量为正的。

3. 介数中心性 Betweenness centrality

介数中心性：

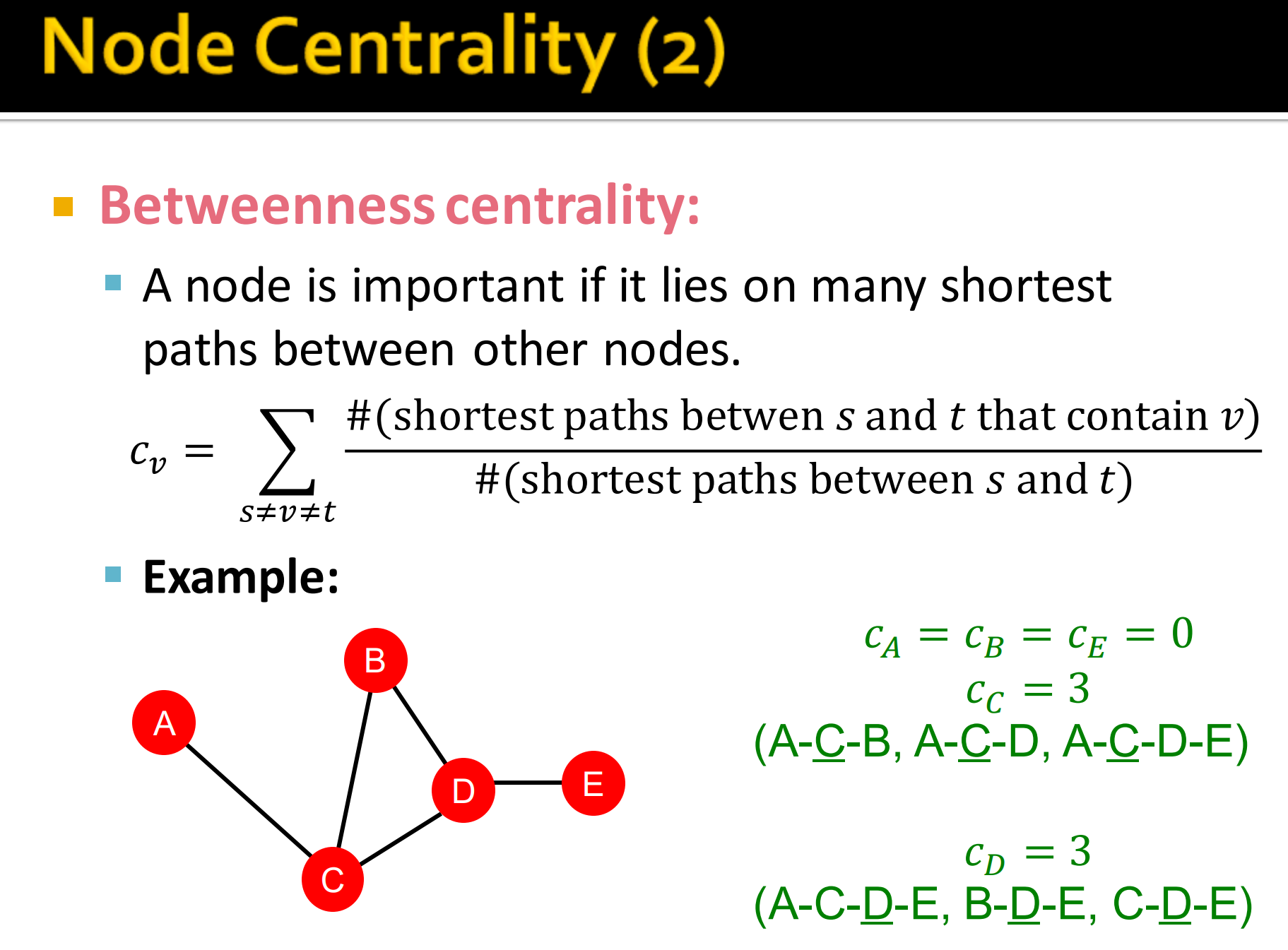
被计算节点处在在任意节点对最短路径的比例，可以理解为对于计算节点，作为被经过的节点组成最短路径的数目与所有路径的比。代表最短路径是否经过该节点。

4. 接近中心性 Closeness centrality

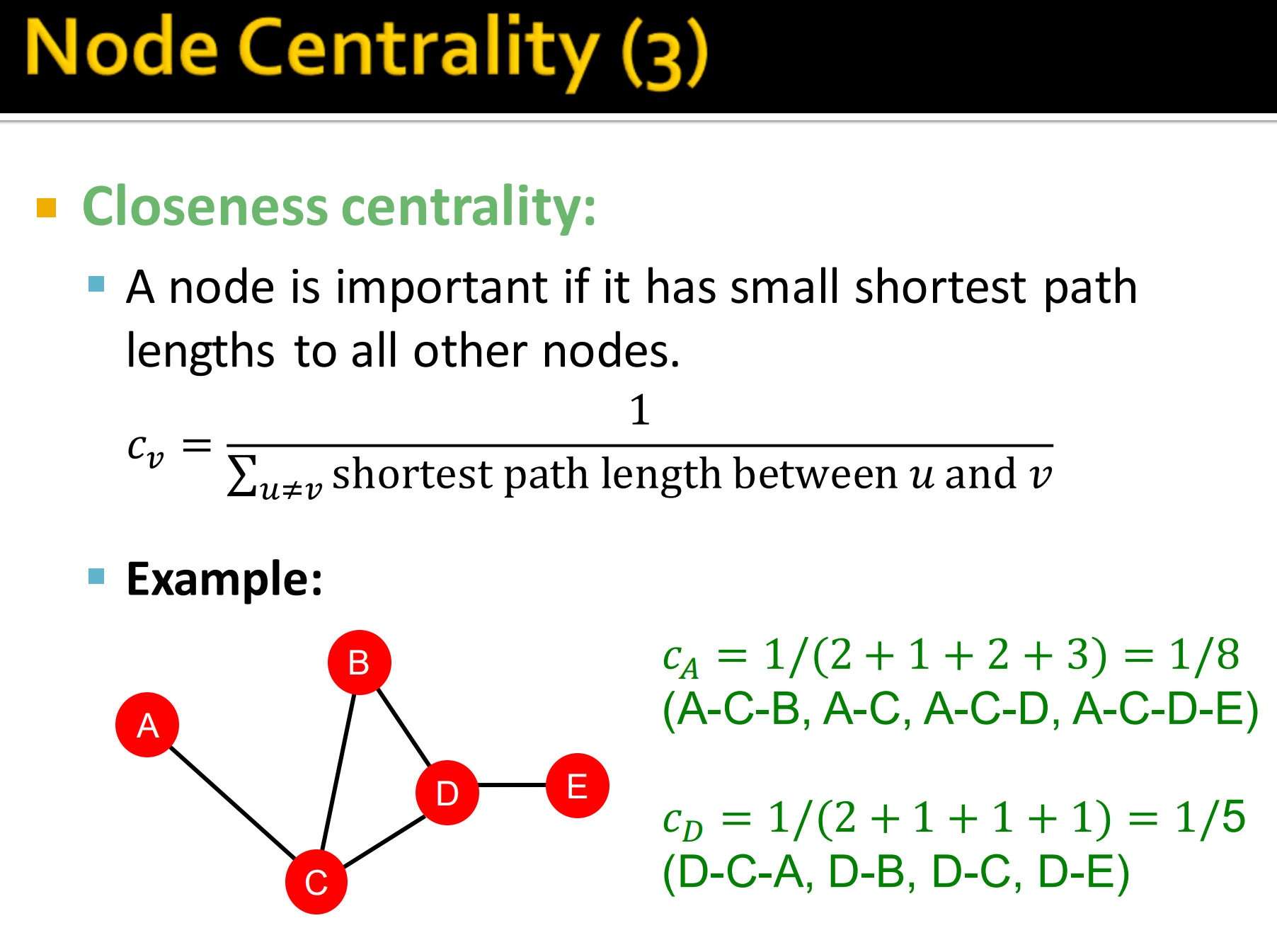
Closeness centrality：如果一个节点是重要的话，那么它到达其它节点的最短路径的总和长度应该是够小的。即:

$c_{v} = \frac{1}{\sum_{u \neq v} \text{v到u的最短路径}} \tag{3}$

如上图例子中, $c_A = 1 / (A到C最短路径+ A到B最短路径+...)=1/(1+2+2+3)=1/8$

5. 节点特征: 聚类系数 Cluster Coefficient

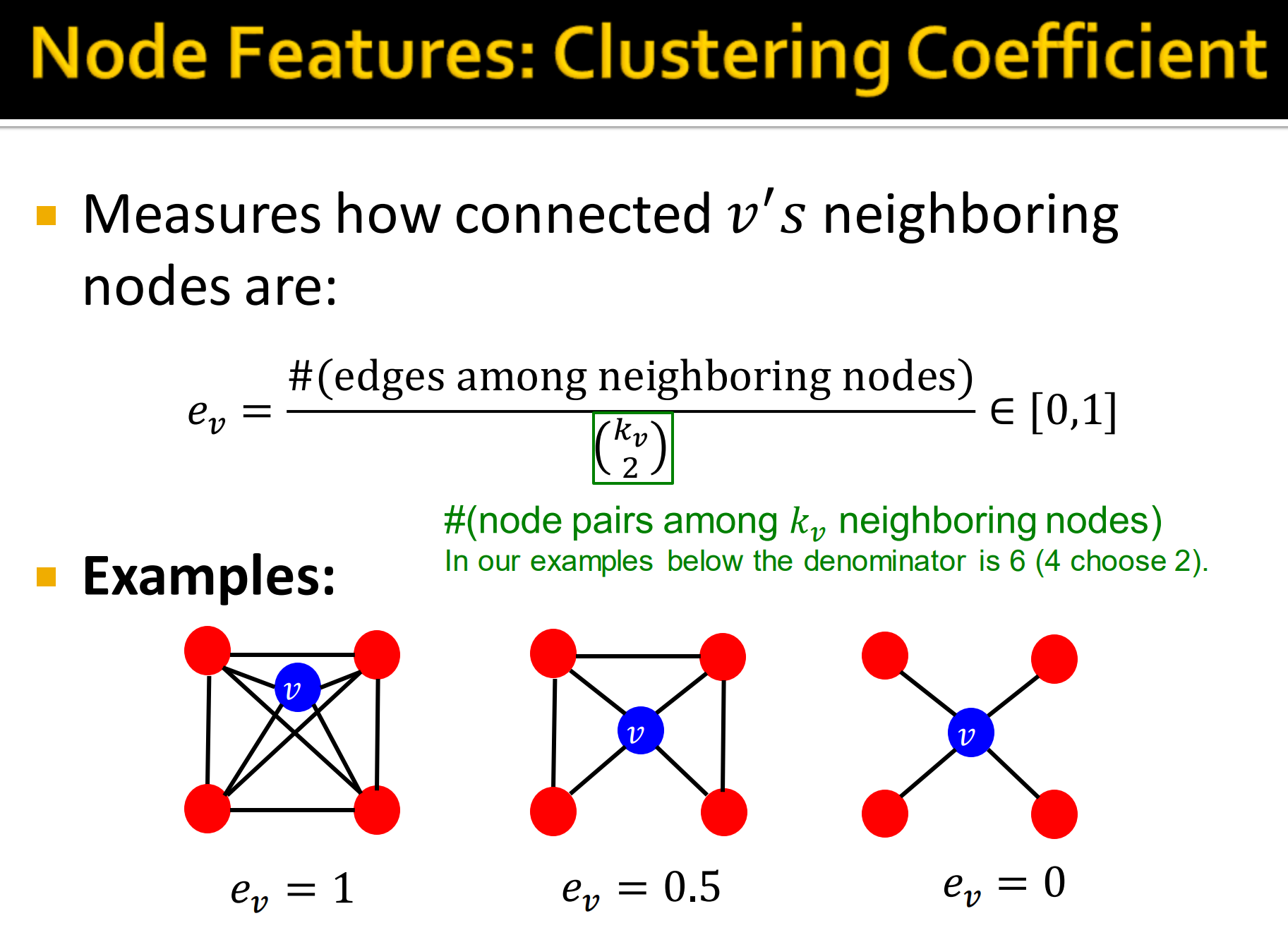
聚类系数: 表示邻居的聚集程度，这个可以一定程度表示图的稀疏程度。

实际上就是算节点v与邻居构成实际组成的三角形数除上最大可能三角形个数。

邻居连接多少边就是多少三角形，这条边连上个自身节点v，就是一个三角形。
随机取两点加上一个不共线的的自身节点v，就是所有可能的三角形。

$e_v = \frac{邻居节点连接边的数目}{C^2_{\text{节点v的邻居数目}}}= \frac{2邻居节点连接边的数目}{\text{节点v的邻居数目}*(\text{节点v的邻居数目}-1)}\tag{4}$

根据式4，

上图中左图 $e_v = \frac{2\times6}{4\times(4-1)}=1$ . 节点v的邻居们连接用了6条边，邻居个数为4. 注意，节点v底下两条边，少了这两条计算结果就是2/3。

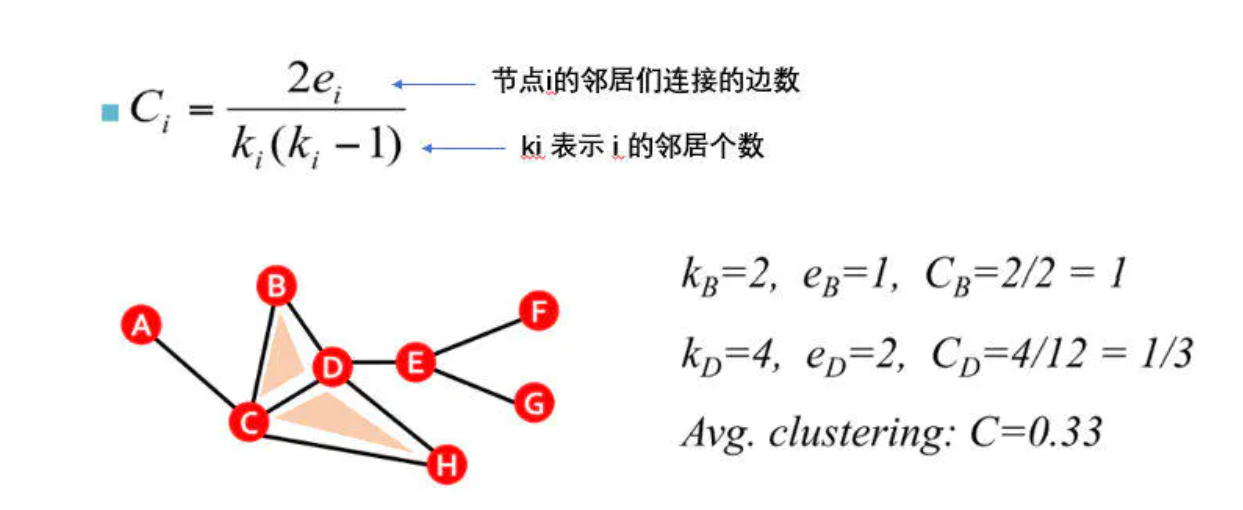
下面有一些计算例子，可以试着计算下。

6. Graphlets 图元

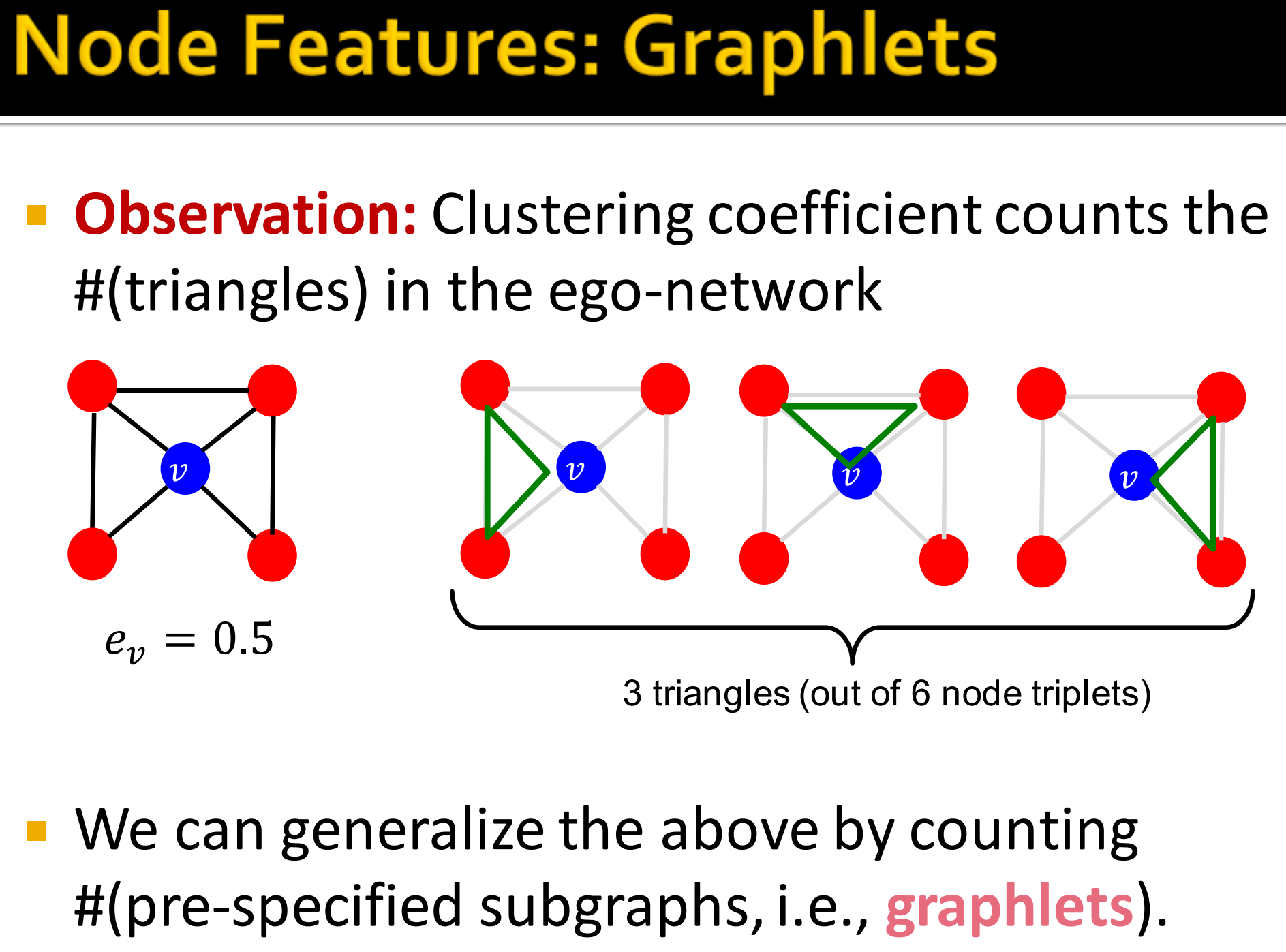
Graphlets: 聚类系数是对ego-network 中三角网络的计算。(这就是为什么解释聚类系数本质在计算实际三角形数目与所有三角形之比。)

所谓的ego network，它的节点是由唯一的一个中心节点(ego)，以及这个节点的邻居(alters)组成的，它的边只包括了ego和alter之间，以及alter与alter之间的边。

我们就可以用一些预指定的子图来替换三角形来计算，聚类系数计算的是三角形网络，我们拓展为图元。

目标: 描述节点u周围的网络结构。

图元是小的子图，描述节点u的邻居节点的结构。

类比：

度：衡量多少节点接触
聚类系数：衡量一个节点接触多少三角形网络
Graphlet Degree Vector(GDV)：节点的基于图元特征。GDV是衡量节点接触的图元数目。

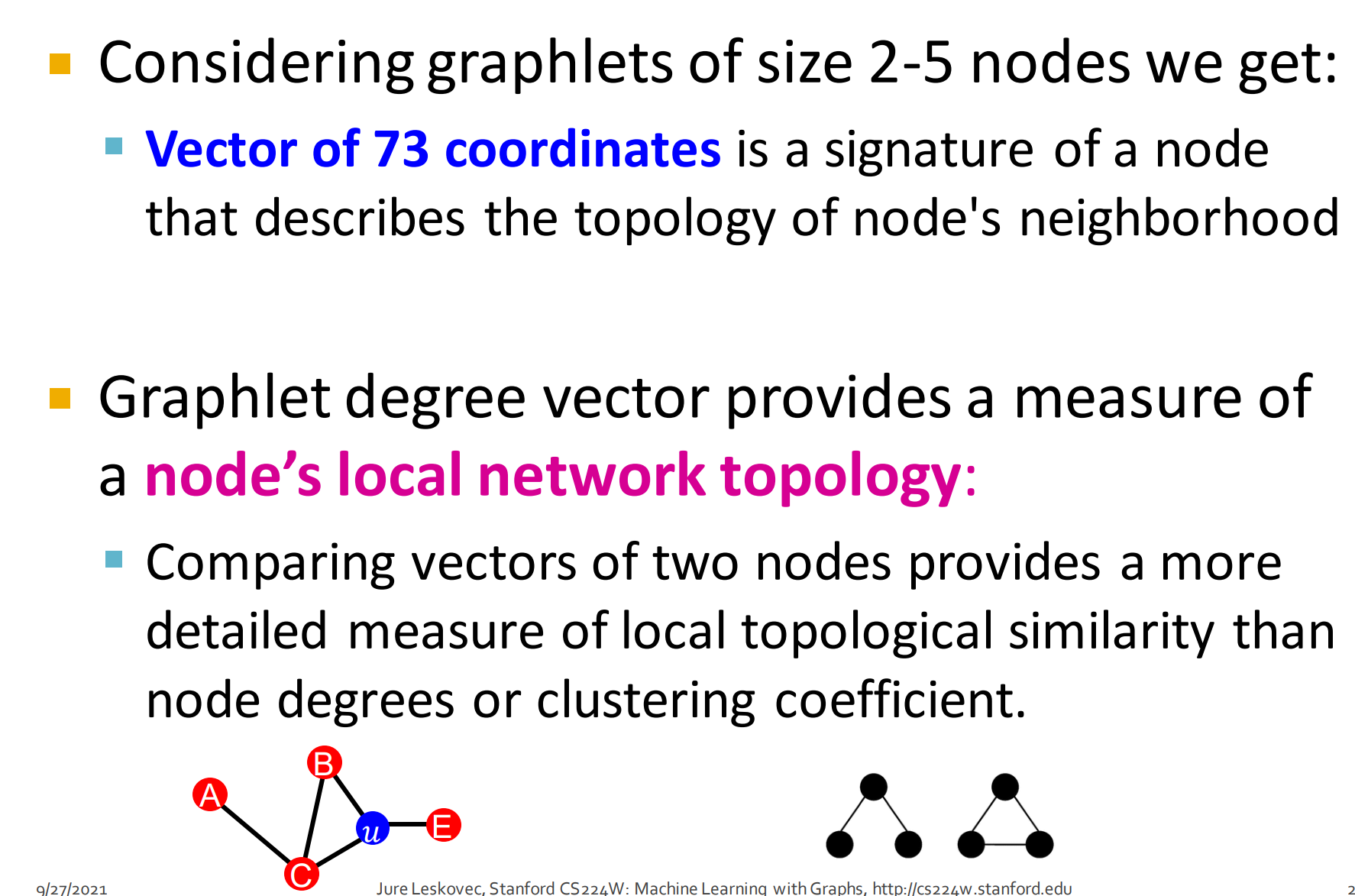
考虑2-5个节点的图元可以获得73个坐标向量: 就是节点记号来描述邻居节点的拓扑
GDV图元度向量可用来一种衡量节点局部网络拓扑结构。
- 相比节点度或聚类系数，比较两个节点的向量(GDV)是一种更详细衡量局部拓扑结构相似度的方法。

7. 导出子图和同构

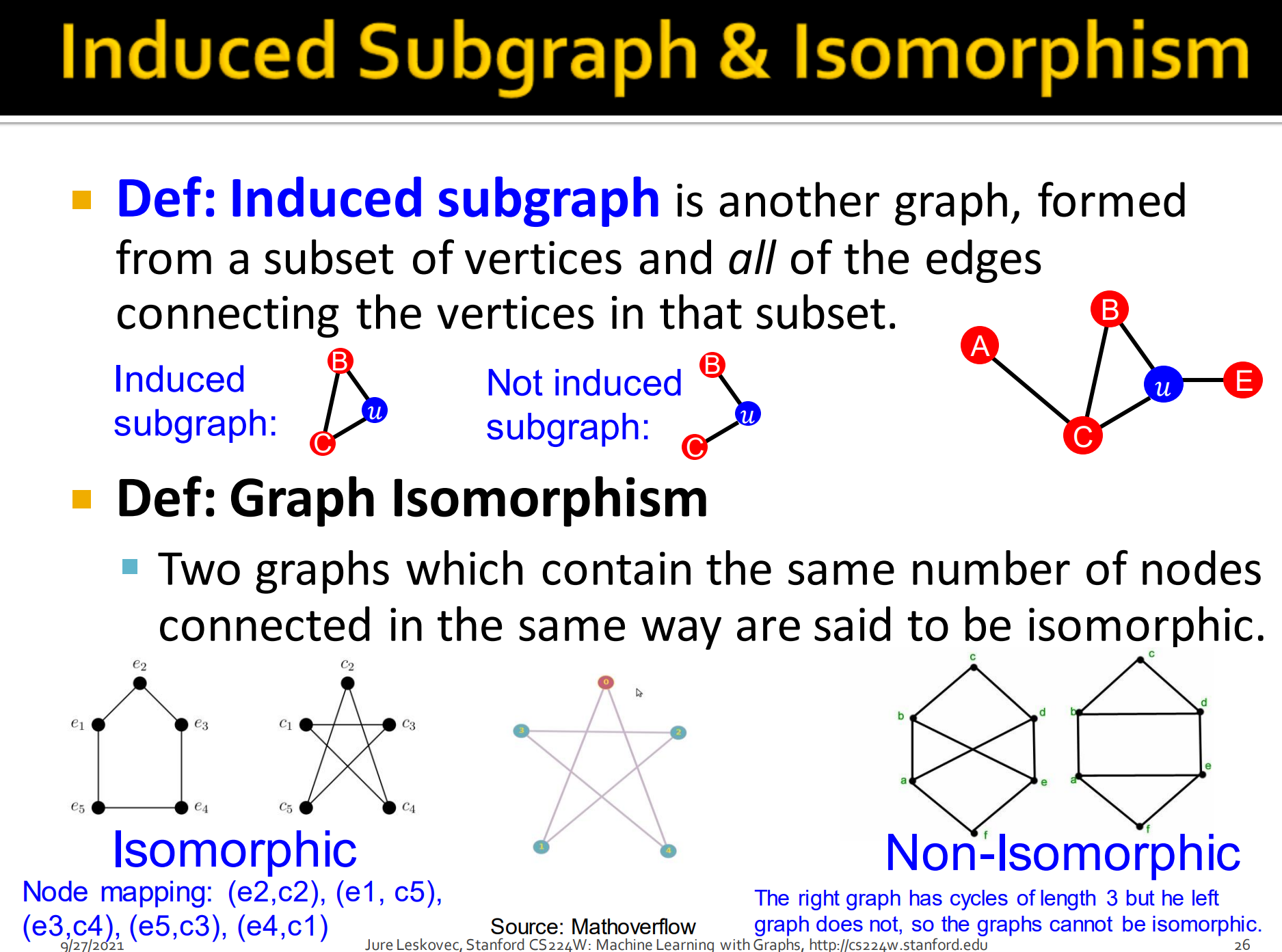
Induced subgraph: 导出子图是另外一种图，由顶点子集和连接该子集中顶点的所有边组成。

上图左边是导出子图，右边不是。是因为左边不包含子集中顶点的所有的边。

Graph Isomorphism，图的同构。同构这个概念来自于群论(主要有个双射概念难理解)，这里定义为两个图包含同样数量的节点，连接方式也一样就说是同构。

知乎回答——怎么理解图的同构?怎么判断两个图是否同构？

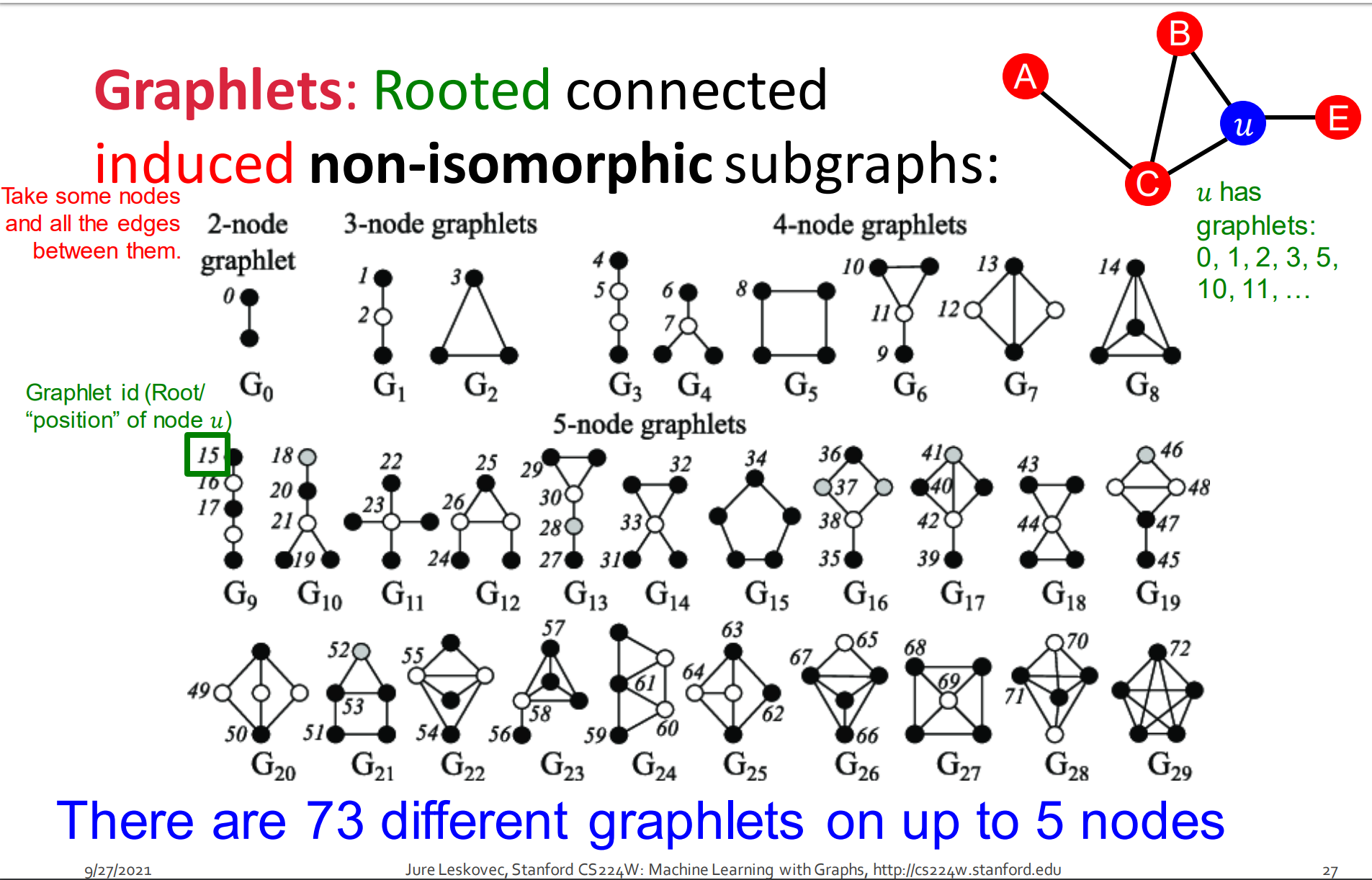
图元是一个有根连接的异构子图。图中标的数字代表根节点可能的位置。例如对于G0，两个节点是等价，这样就一个标号。

到5个节点一共能产生如图所示73种graphlet。

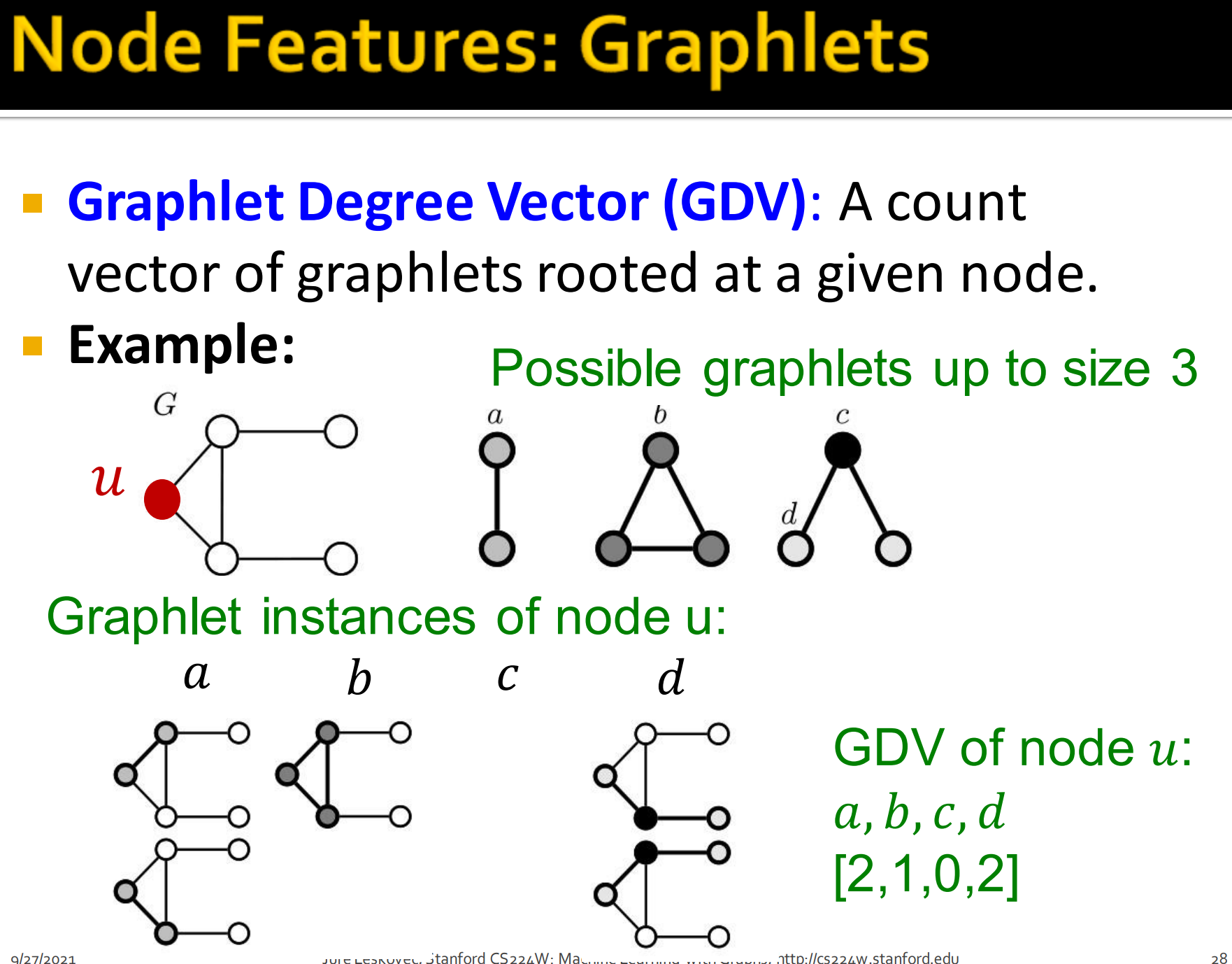
Graphlet Degree Vector (GDV): 以给定节点为根的图元计数向量。

如上图，给定u节点的可能有图元a， b, c, d.拿到原图(红色u节点图)去匹配得出，a有2，b有1，c有0，d有2.这样节点u的GDV就是[2, 1, 0, 2].

8.节点级别特征总结

基于重要性的特征: 获取图中节点的重要性
- 节点度: 简单统计邻居节点数目
- 不同节点中心性衡量:
  - 衡量图中邻居节点重要性
  - 不同衡量选择：特征值中心性，中介中心性，接近中心性
基于结构的特征
- 节点度: 简单统计邻居节点数目
- 聚类系数: 衡量跟邻居节点怎么连接
- 图元计数向量：统计不同图元出现的频率

4. Link-level prediction

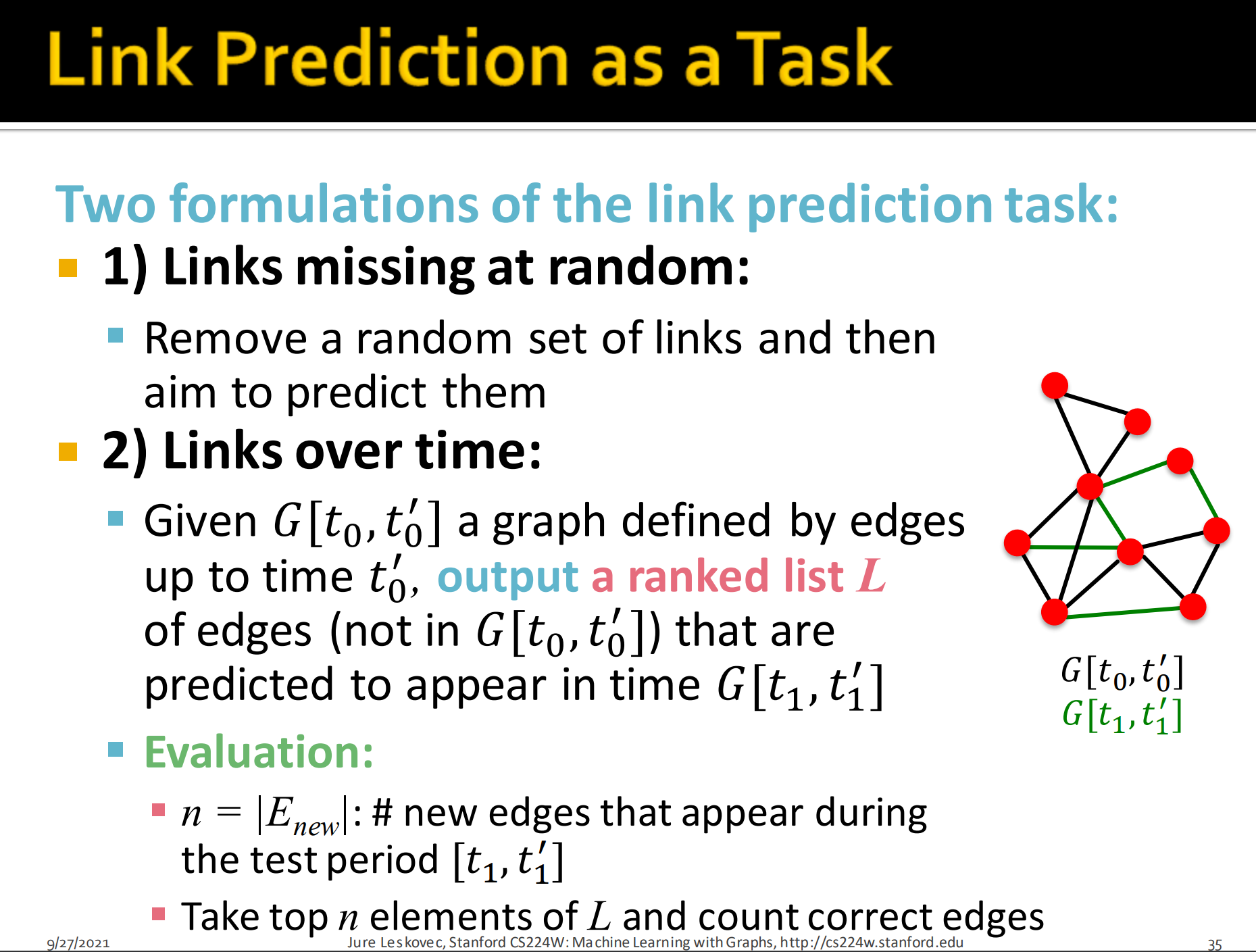
边预测任务两种公式化：

随机缺失边
- 随机覆盖一些边，然后预测两个节点间是否会连接，2分类问题。
边随时间演化
- 给定 $G[t_0, t^{\prime}_0]$ , 即给定 $t_0 \ 到 \ t^{\prime}_0$ 的边连接确定的图，预测未来 $G[t_1, t^{\prime}_1]$ 边连接情况，输出即一个排序的list L. 如推荐中，我们用1月份用户A关注的数据预测2月份关注情况，来进行推荐。
- 评估：
  - $n=|E_{\text{new}}|$ : 测试时期 $[t_1, t^{\prime}_1]$ 新边出现的次数。
  - 取输出list L 的前n个元素，并对正确预测的边计数。

1. Link Prediction via Proximity

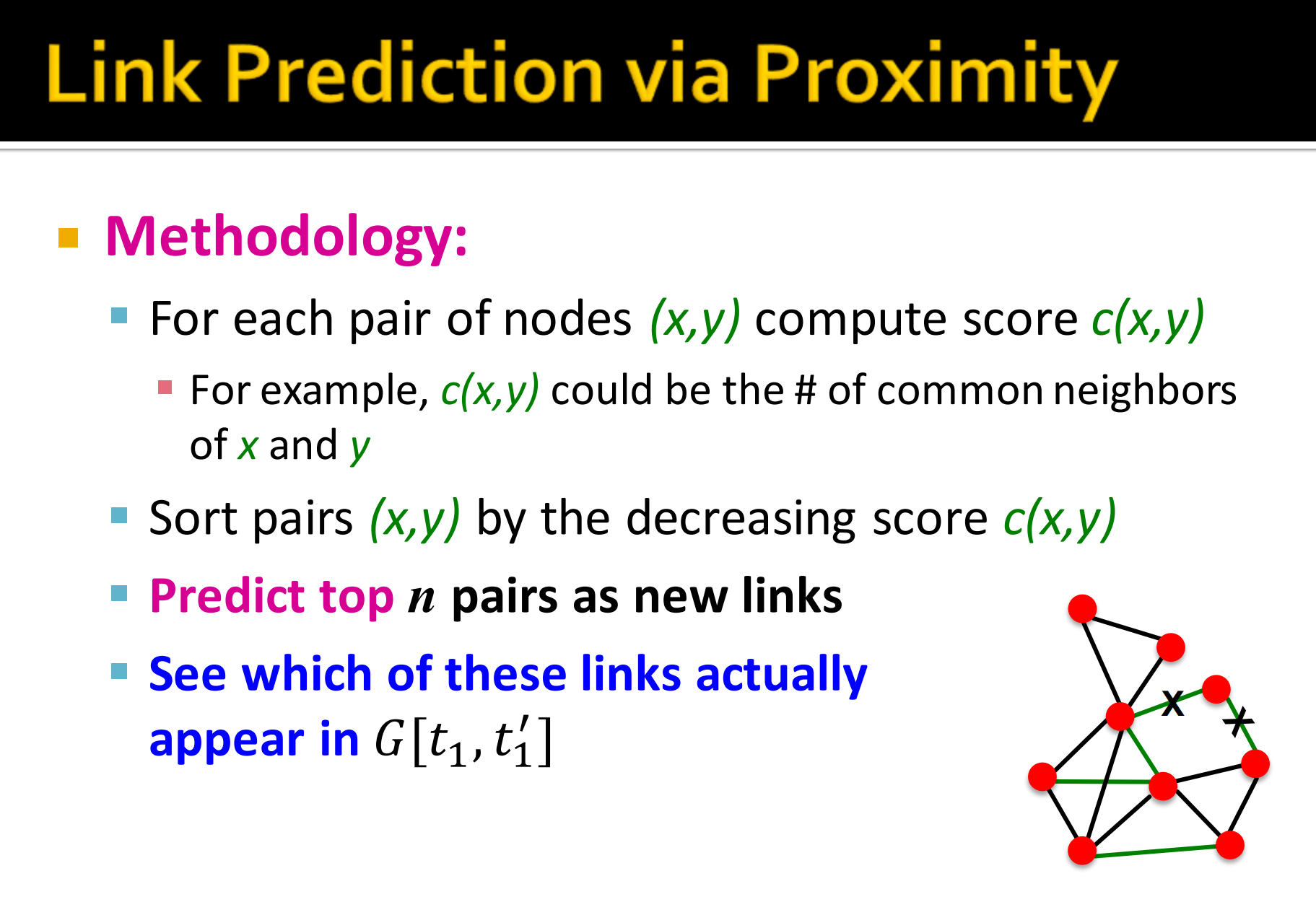
方法
- 对于每个节点对就是那分数
  - 例如， $c(x, y)$ 是 $x , \ y$ 共同的邻居数目
  - 按照 $c(x, y)$ 分数来对 $(x, y)$ 对排序
  - 预测前n对作为新的连接
  - 评估时看哪些边真正在 $G[t_1, t_1^{\prime}]$ 时出现。

2. 边级别特征：概述

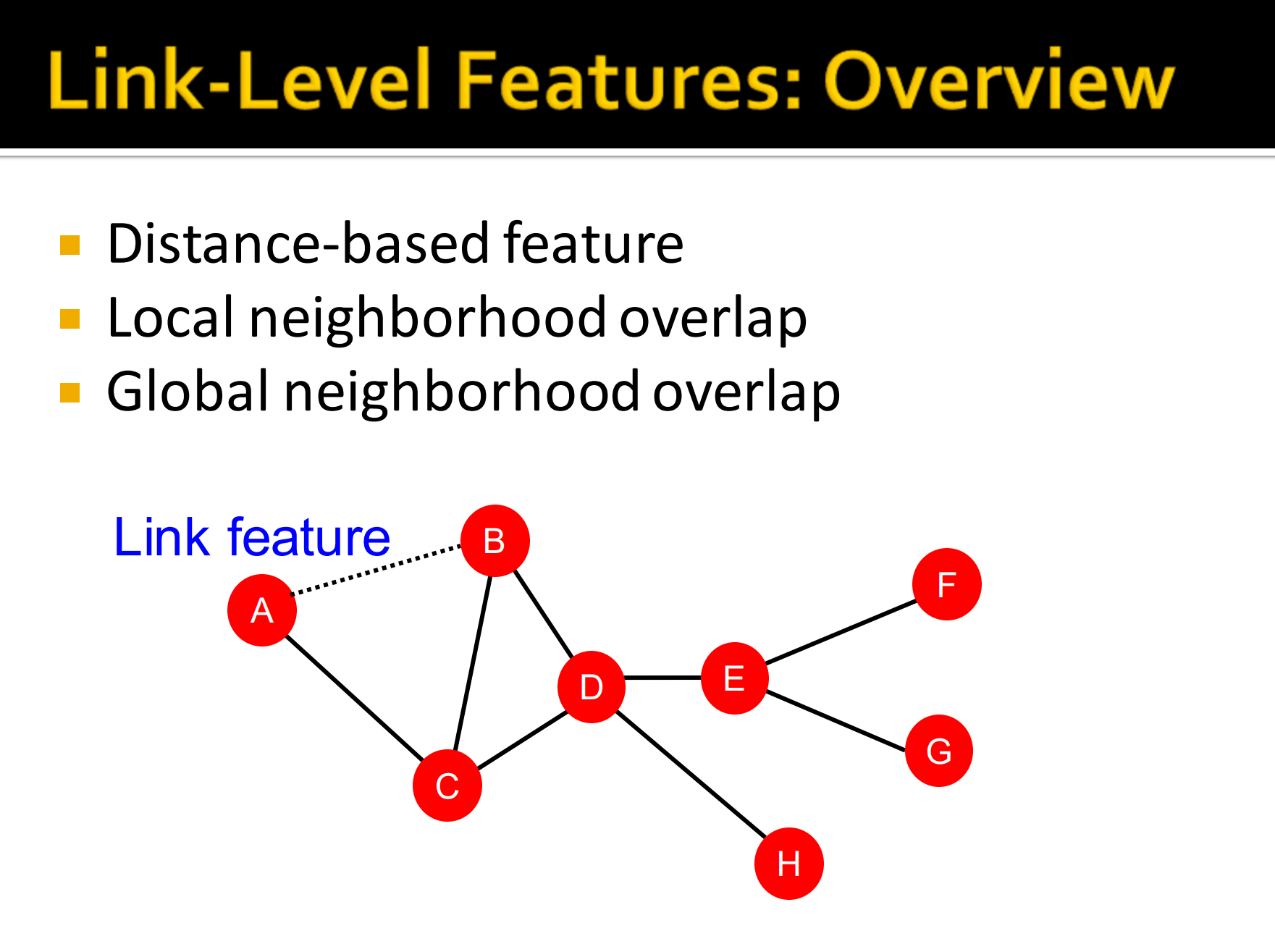
基于距离的特征
局部邻居重叠
全局邻居重叠

基于距离特征的不合理之处：

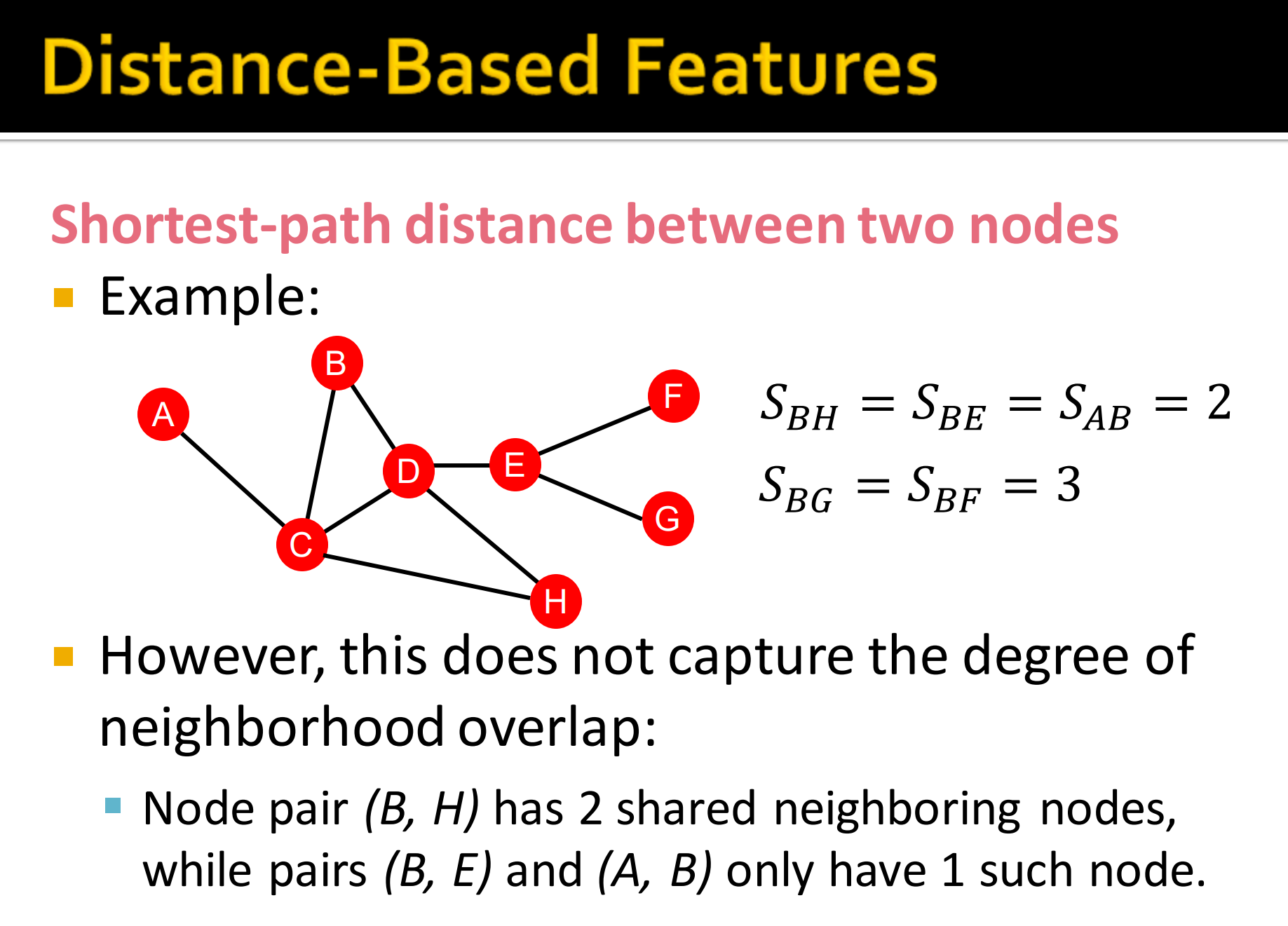
如上图中，BH直接最短距离为2，BE也为2.但BH有2个共享的邻居节点，BE只有一个。不能表现图结构的具体信息。因此我们就引入neighborhood overlap。

3. 局部邻居节点重叠

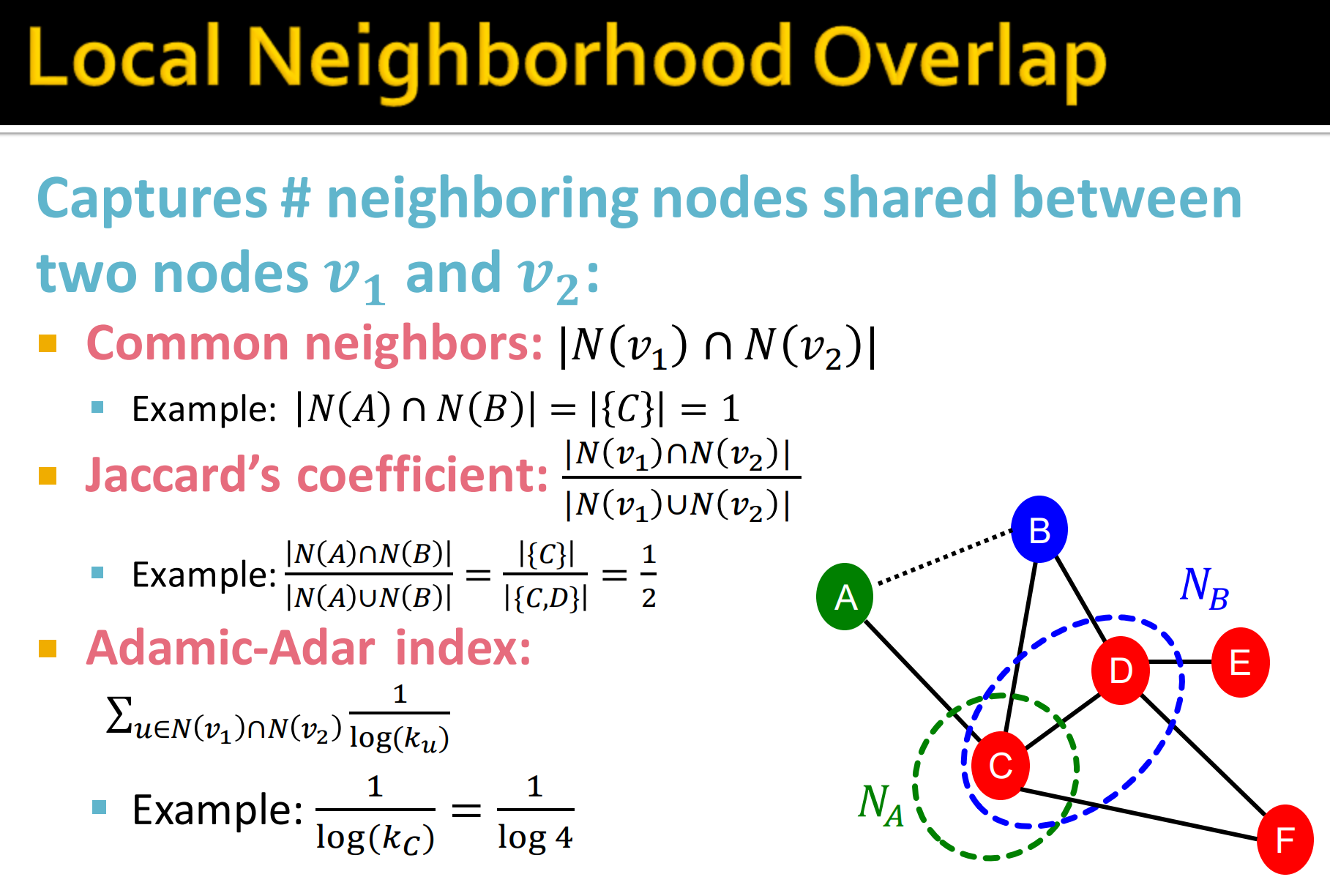
直接看共同邻居节点:

$f(v_1, v_2) = |N(v_1)\cap N(v_2)| \tag{5}$

Jaccard’s coefficient

$f(v_1, v_2) = \frac{ |N(v_1)\cap N(v_2)|}{ |N(v_1)\cup N(v_2)|} \tag{6}$

Adamic-Adar index：

$\sum_{u\in N(v_1) \cap N(v_2)} \frac{1}{\log(k_u)} \tag{7}$

其中 $\log(k_u) 表示\ v1, \ v_2$ 公共的邻居节点的度，即所有邻居节点的度的对数的倒数的和。

4. 全局邻居节点重叠

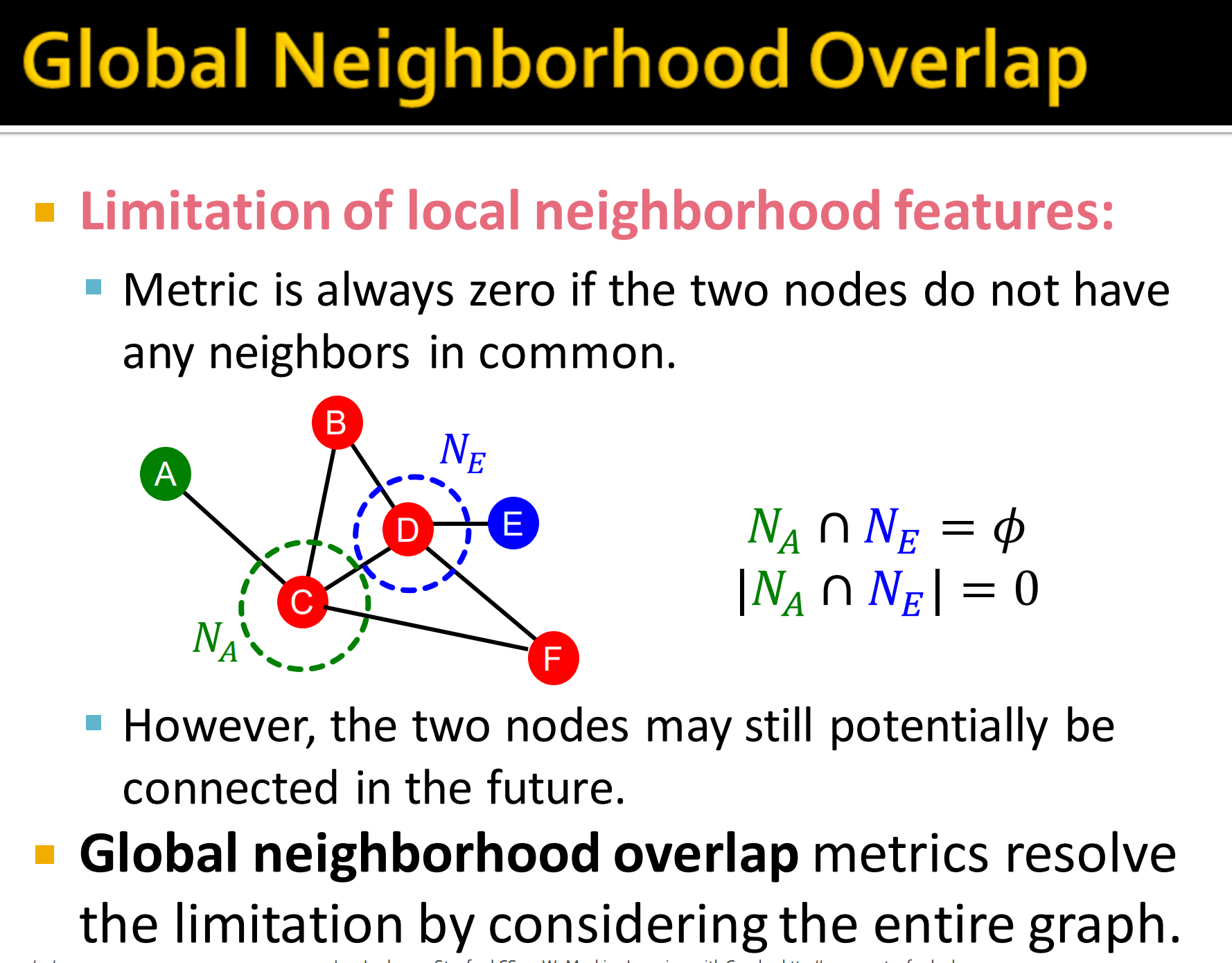
Local neighborhood features 的限制
- 评价指标总是0如果两个节点没有任何共同的邻居节点
- 然而，两个节点可能在将来会连接
Global neighborhood overlap 评价指标考虑整个图能解决这个限制

5.全局邻居节点重叠指标

Katz index: 最基本的全局指标，给定一对节点，对其走过的所有路径长度计算，即计算节点对的各个路径长度下的路径数量。katz指标易受到节点度数的影响，度数越高的节点，其路径越多，取值越大。
那么怎么计算？——使用邻接矩阵计算。

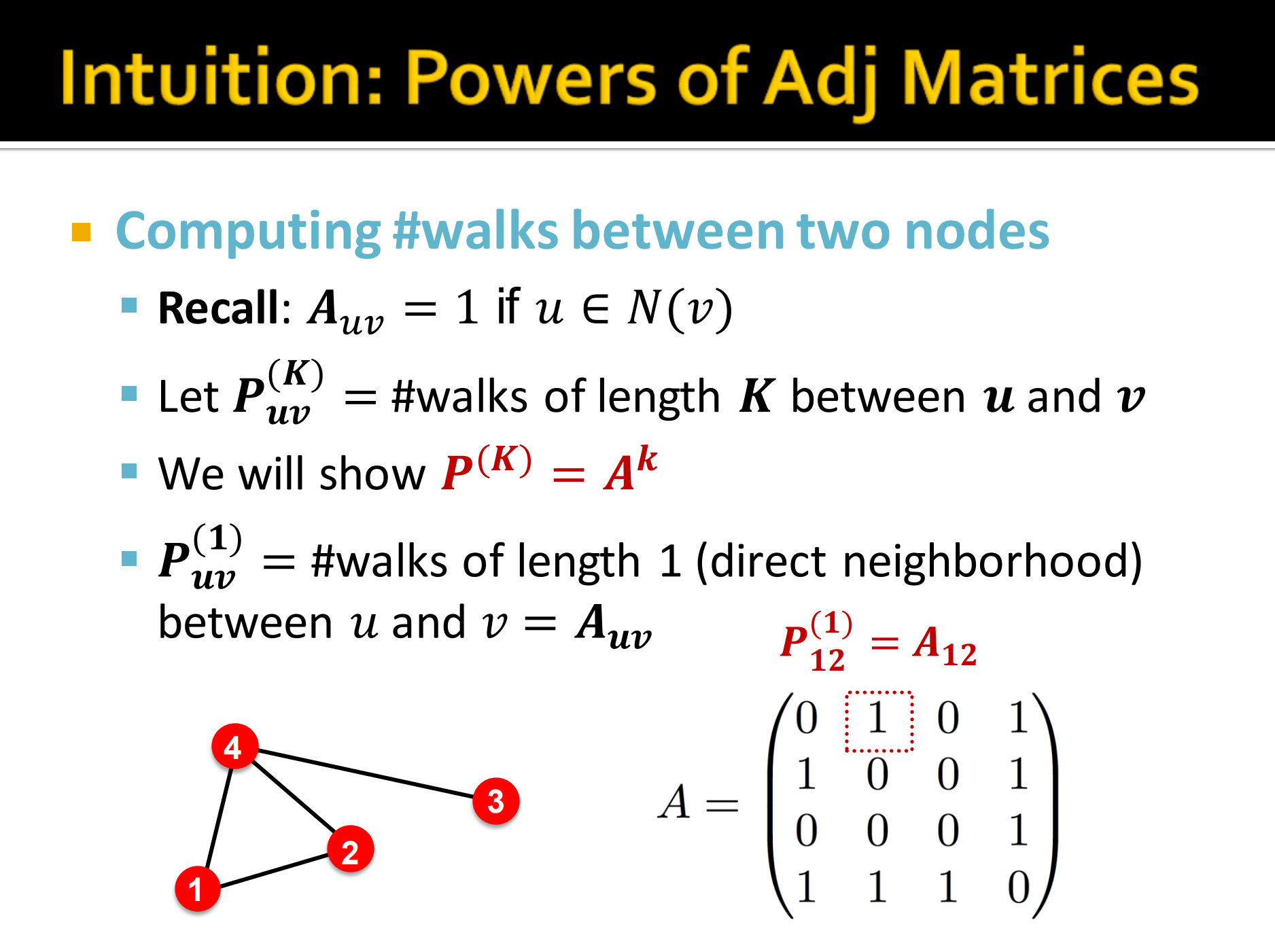
直觉：利用邻接矩阵的幂。

Recall: 对应 $\mathbf{A}_{uv}=1, \ 其中 \mathbf{u} 是 \mathbf{v}的邻居节点, 即\text{if} \ \mathbf{u}\in N(\mathbf{v})$ 。相连为1嘛。
记 $\mathbf{P}_{uv}^{(K)}$ 为u和v直接的路径长度。
接下来我们证明 $\mathbf{P}^{(K)}_{uv} = \mathbf{A}^k$ 。
因为 $\mathbf{P}^1_{uv}$ 表示u和v之间的路径长度为1，即直接的邻居节点。这时候，就变成了 $\mathbf{P}^1_{uv}=\mathbf{A}_{uv}$ ,简单来说就是对应的邻接矩阵。

那么怎么计算 $P^{(2)}_{\mathbf{u}\mathbf{v}}$ ?（我们要计算2步从u跳到v的所有路径，先跳1步再怎么1步跳到v。）

Step 1: 计算每个 $\mathbf{u}的邻居节点和\ \mathbf{v}$ 之间的所有长度为1的路径数
Step 2: 对经过 $\mathbf{u}$ 的邻居节点路径求和
写成公式就是 $P^{(2)}_{\mathbf{u}\mathbf{v}} = \sum_i \mathbf{A}_{ui} * \mathbf{P}^{(1)}_{iv}$ ，这里i代表u的邻居节点，再回过去看1,2步公式。最后可得就是邻接矩阵的幂次运算，其中幂次代表长度。

6. Katz index

Katz index：对节点对之间所有长度的路径数量进行了统计计数。

那么怎么计算两个节点间路径?

邻接矩阵的幂
- $\mathbf{A}_{uv}$ 表示u和v之间长度为1的路径，直接的邻居节点。(跳1步)
- $\mathbf{A}_{uv}^2$ 表示 u和v之间长度为2的路径，邻居的邻居。(跳2步)
- 那么 $\mathbf{A}_{uv}^l$ 就是长度为l的路径。(跳l步)

公式: $v_1 \ 和 v_2$ 之间所有长度的路径求和。

$S_{v_1v_2} = \sum_{l=1}^{\infty} \beta^l \mathbf{A}_{v_1v_2}^l \ \ \ 其中, 0 \lt \beta \lt 1\tag{8}$

其中 $0 \lt \beta \lt 1$ 为自定义权重衰减因子，邻居节点赋予不同的权重, 对于短路径赋予较大的权重, 而长路径赋予较小的权重。

证明: 简单地展开有:

$S=\beta A + \beta^2 A^2 + \cdots + \beta^n A^n \tag{9}$

转换下形式推导:

$\begin{align} &(I-\beta A)(I+S)\\ &=(I-\beta A)(I + (\beta A + \beta^2 A^2 + \cdots + \beta^n A^n ))\\ &=I - \beta A + (\beta A + \beta^2 A^2 + \cdots + \beta^n A^n ) - \beta A (\beta A + \beta^2 A^2 + \cdots + \beta^n A^n )\\ &= I +(\beta^2 A^2 + \cdots + \beta^n A^n) -(\beta^2 A^2 + \cdots + \beta^n A^n + \beta^{n+1} A^{n+1})\\ &= I \end{align} \tag{10}$

由式10易得:

$S = (I-\beta A) ^{-1} - I \tag{11}$

7. 边级别特征：总结

基于距离的特征
- 用两个节点间最短的路径，但不能获取邻居节点是怎么重叠
局部邻居节点重叠
- 获取两个节点间多少公共的邻居节点
- 容易变成0，没有公共邻居节点共享
全局邻居节点重叠
- 用全局图结构来对两个节点打分
- Katz index: 对两个节点间所有路径长度计数(就把所有路径长度一起求和)

5. 图级别特征

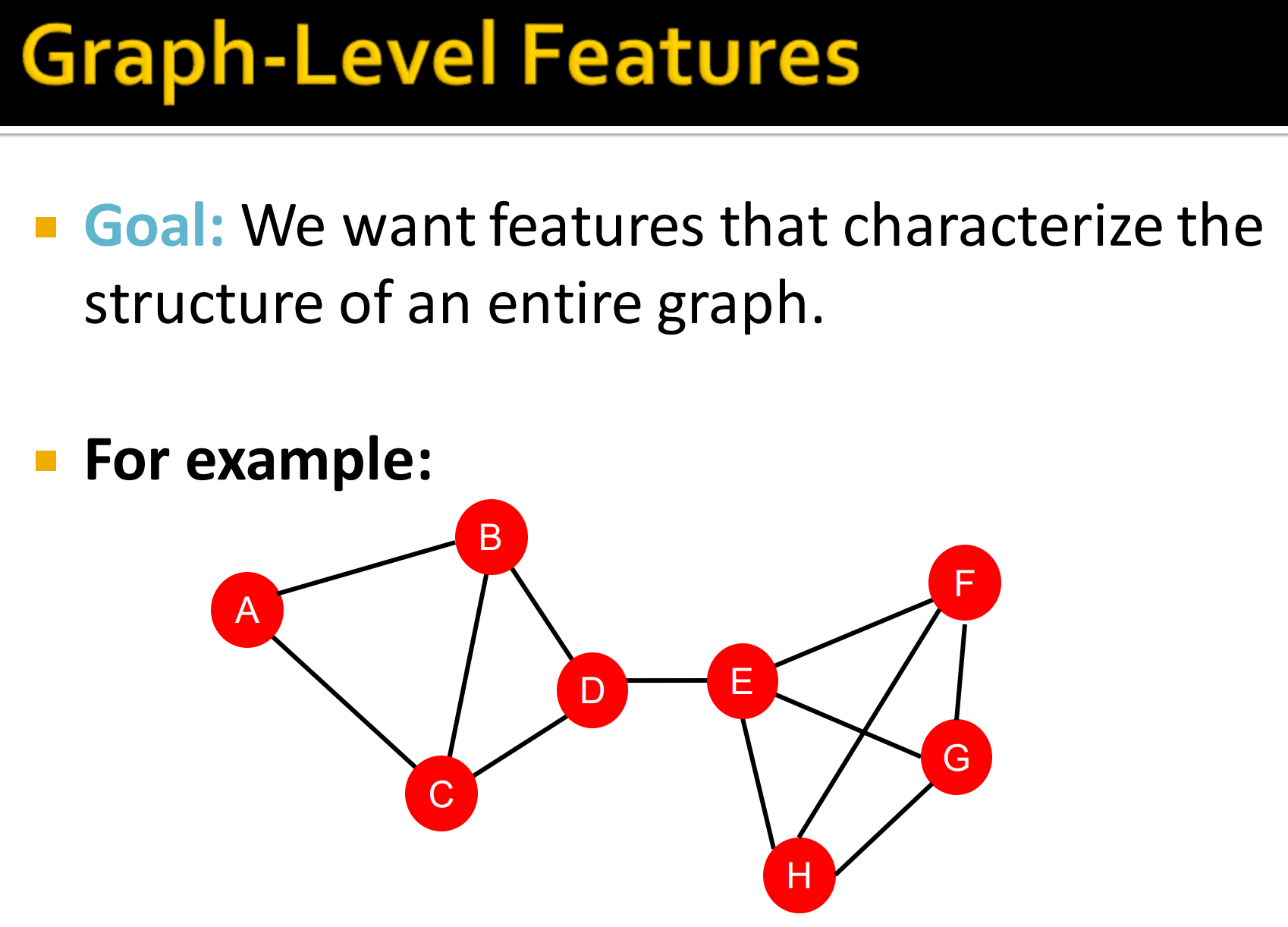
目标: 表征整个图结构

背景: Kernel Methods

Kernel method 在图级别预测的传统机器学习中广发运用
Idea: 设计kernel来替换掉特征向量，跟机器学习中的核方法作用一样，比如SVM中核技巧
Kernel简介:
- Kernel $K(G, G’) \in \mathbb{R}$ 衡量 b/w 数据的相似性
- Kernel matrix $K = (K(G, G^\prime))_{G, G^{\prime}}$ , 必须是半正定, 要其有正的特征值。
- 存在特征表达式 $\phi(\cdot)$ ，使得 $K(G, G^\prime) = \phi(G)^T \phi(G^{\prime})$
- kernel 一旦定义，就可以使用现成的ML模型如核SVM，进行预测。

1. 图级别特征：概述

Graph Kernels：衡量两个图的相似度
- Graphlet Kernel
- Weisfeiler-Lehman Kernel
- 其它的kernel: Random-walk kernel, Shortest-path graph kernel…

2. Graph Kernel : Key Idea

目标：设计图特征向量 $\phi(G)$ .
Key idea：图的Bag-of-Words(BoW)
- Recall: BoW简单利用词的数目作为文档特征(不考虑顺序)。
- 简单拓展到图: 将每个节点看作BoW中的词。
- 像如果两个4红色节点的图，经过同一 $\phi$ 处理后提取的特征向量一样。

上面已经说到用指定数目的节点的图过核函数 $\phi$ 来获取特征向量，再进一步将其转换为节点的度。就变成了：我们使用节点度的“Bag”.

向上图中，我们得到的两个4节点的图经过核函数后得到的不同特征向量。这样是不行的。

所有的Graphlet Kernel 和 Weisfeiler-Lehman(WL) 使用图的Bag-of- *表征，这里星号是比节点度更广泛的东西。

3. Graphlet feature

关键点：就是拿图元作为模板(pattern),去匹配图中出现对应图元对应数目。

注：这里定义的图元跟节点级别的特征有2点区别。

这里图元中节点不需要被连接，可以是孤立的点
这里的图元没有根

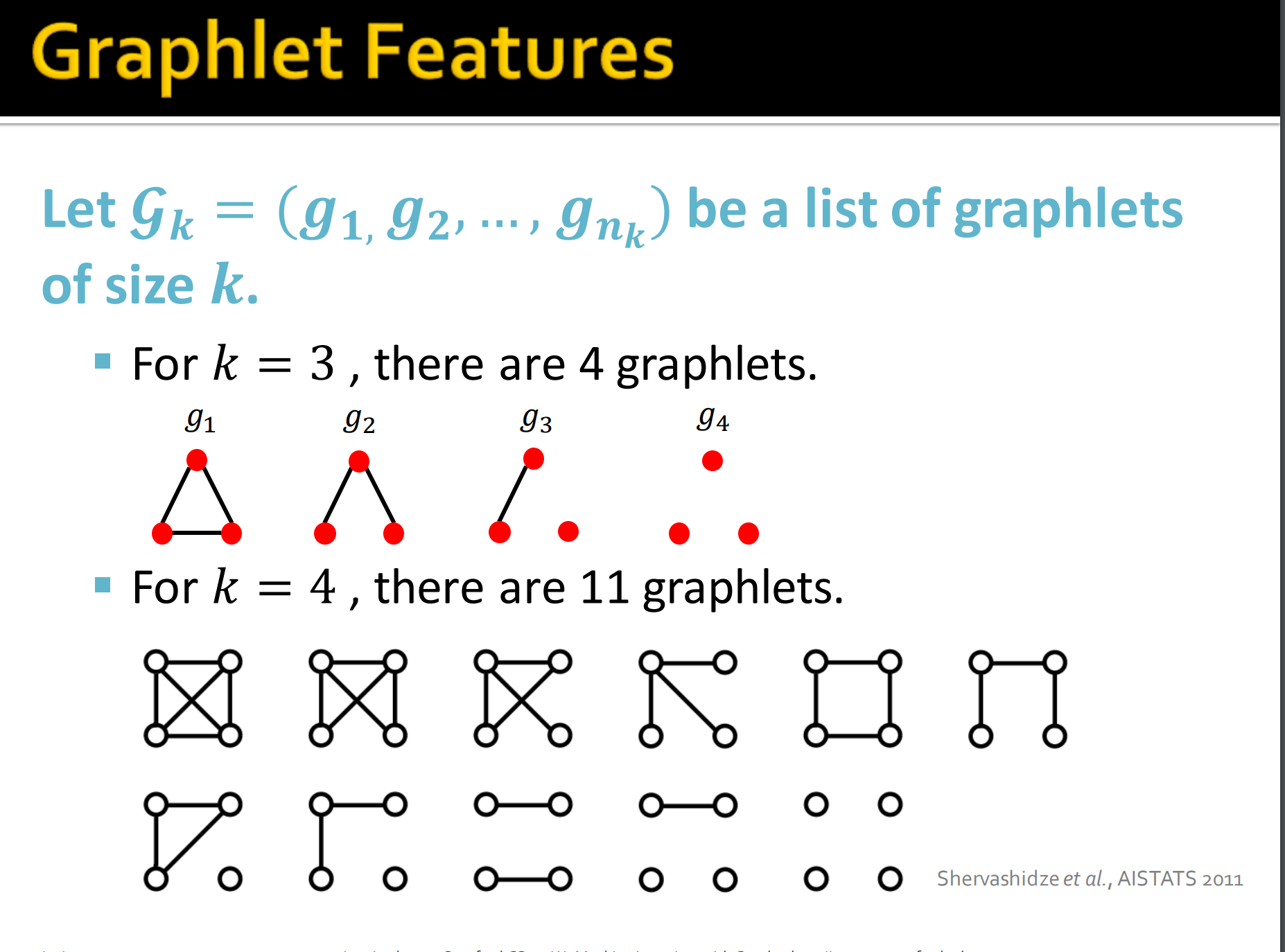
令 $G_k = (g_1, \cdots, g_{n_k})$ ，表示k个节点内的图元的列表。

例如，k=3，就因为可以是孤立的点，图元数目比节点图元数多。同样也没有根这个概念了。

那么就有如下定义：给定图 $G$ ,以及图元列表 $\mathcal{G}_k = (g_1, g_2, \cdots, g_{n_k})$ .那么图元数目向量 $\mathcal{f}_G \ \mathbb{R}^{n_k}$ 如上图所示, 表示：

$(\mathcal{f}_G)_i$$等于属于G的图元$$g_i$$的数目，这样就构成一个向量。 <img src="https://aigonna.oss-cn-shenzhen.aliyuncs.com/blog/202205011912512.png" alt="image-20220321180458265" style="zoom:25%;" /> 如上所示例子中，图元$$g_1$$在图中匹配一个，其它依次匹配为3， 6， 0，所以该向量为$$\mathcal{f}_G = (1, 3, 6, 0)^T$$。 ##### 4. Graphlet Kernel <img src="https://aigonna.oss-cn-shenzhen.aliyuncs.com/blog/202205011912060.png" alt="image-20220321180757475" style="zoom:25%;" /> - 给定两个图$$G, \ G^\prime$$，graphlet kernel 计算为:$

K(G, G^{\prime}) = \mathbf{f}G\ ^T \mathbf{f}{G^\prime}\tag{12}

$- 问题:如果两个图size差非常多，那么将会导致乘积也非常大。 - **Solution**：归一化所有向量。 <img src="https://aigonna.oss-cn-shenzhen.aliyuncs.com/blog/202205011913100.png" alt="image-20220321223918765" style="zoom:25%;" /> **限制**：枚举图元是非常昂贵的！ - 对n大小的图枚举k大小的图元，需要$$n^k$$次 - 这将会不可避免最坏的情况出现，因为子图同构测试(判断一个图和另外一个图是否同构)是NP-hard问题。 - 如果一个图节点度被限制为d，存在复杂度为$$O(nd^{k-1})$$统计所有size为k的图元的算法. 那我们能设计一个更有效的graph Kernel吗？ ##### 5. Weisfeiler-Lehman Kernel <img src="https://aigonna.oss-cn-shenzhen.aliyuncs.com/blog/202205011913035.png" alt="image-20220321225746090" style="zoom:25%;" /> - 目标:设计高效的图特征描述器$$\phi(G) $$. - **想法**: 利用邻居节点结构来迭代丰富节点词汇表 - **Bag of node degrees**的广义版本，因为节点度只是one-hop邻居信息，这可以包括更多跳(路径长度更长)信息。 - 算法的实现**颜色细化(Color refinement)**。算法也称为**Weisfeiler-Lehman graph isomorphism test(Weisfeiler-Lehman图同构检验)。** ##### 6. Color Refinement <img src="https://aigonna.oss-cn-shenzhen.aliyuncs.com/blog/202205011913428.png" alt="image-20220321234711813" style="zoom:25%;" /> - 给定一个图G，其有一系列节点V。 1. 分配每个节点v一个初始颜色$$c^{(0)}(v)$

按以下公式迭代改进节点颜色

$c^{(k+1)}(v) = \text{HASH}( \{c^{k}(v), \{c^{(k)}(u)\}\}_{u \in N(v)}) \tag{13}$

HASH表示哈希函数，将不同输入映射到不同颜色。

3. 在K步后，分配的颜色包含了$$c^{(K)}(v)$$ K阶近邻的信息。

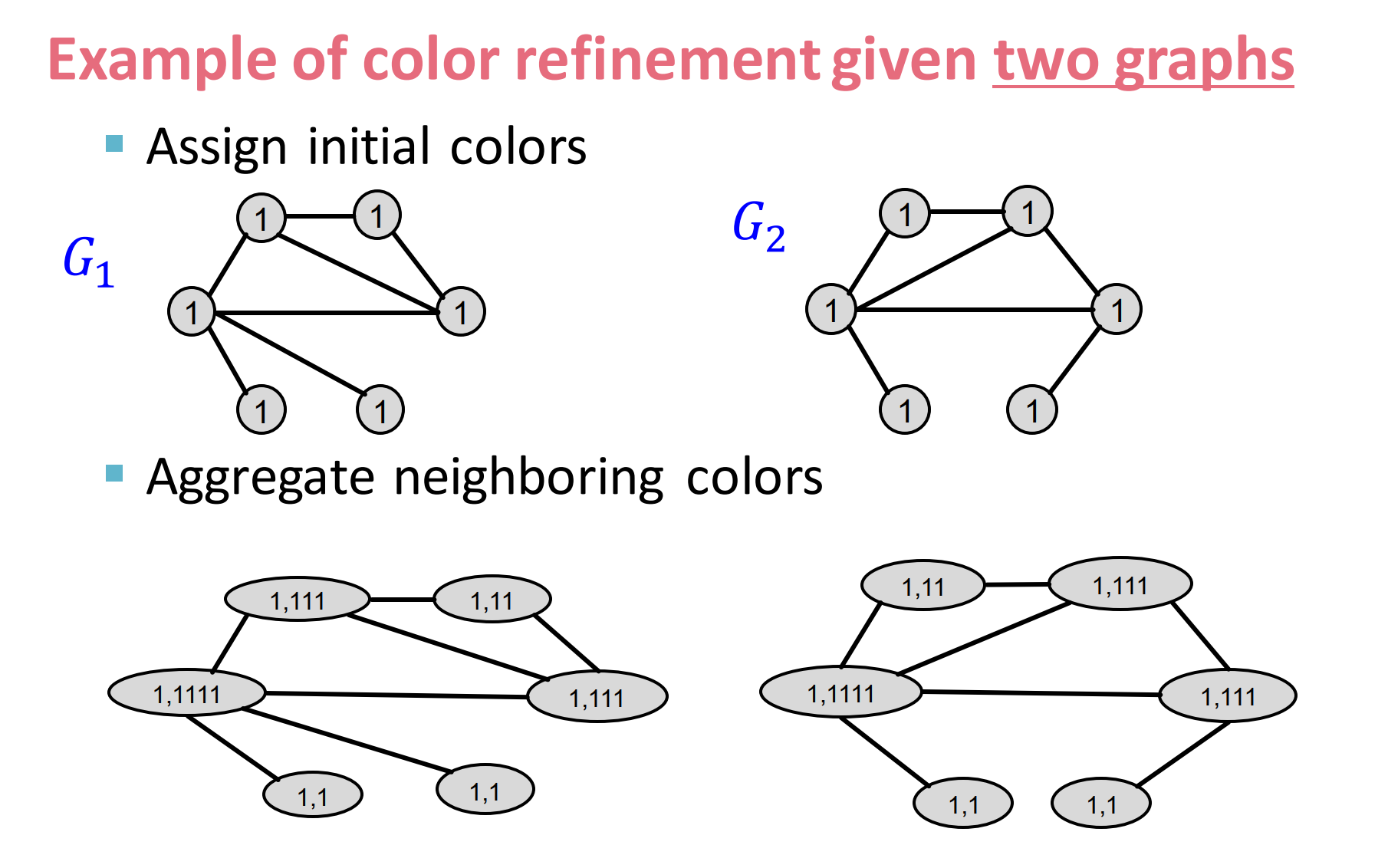
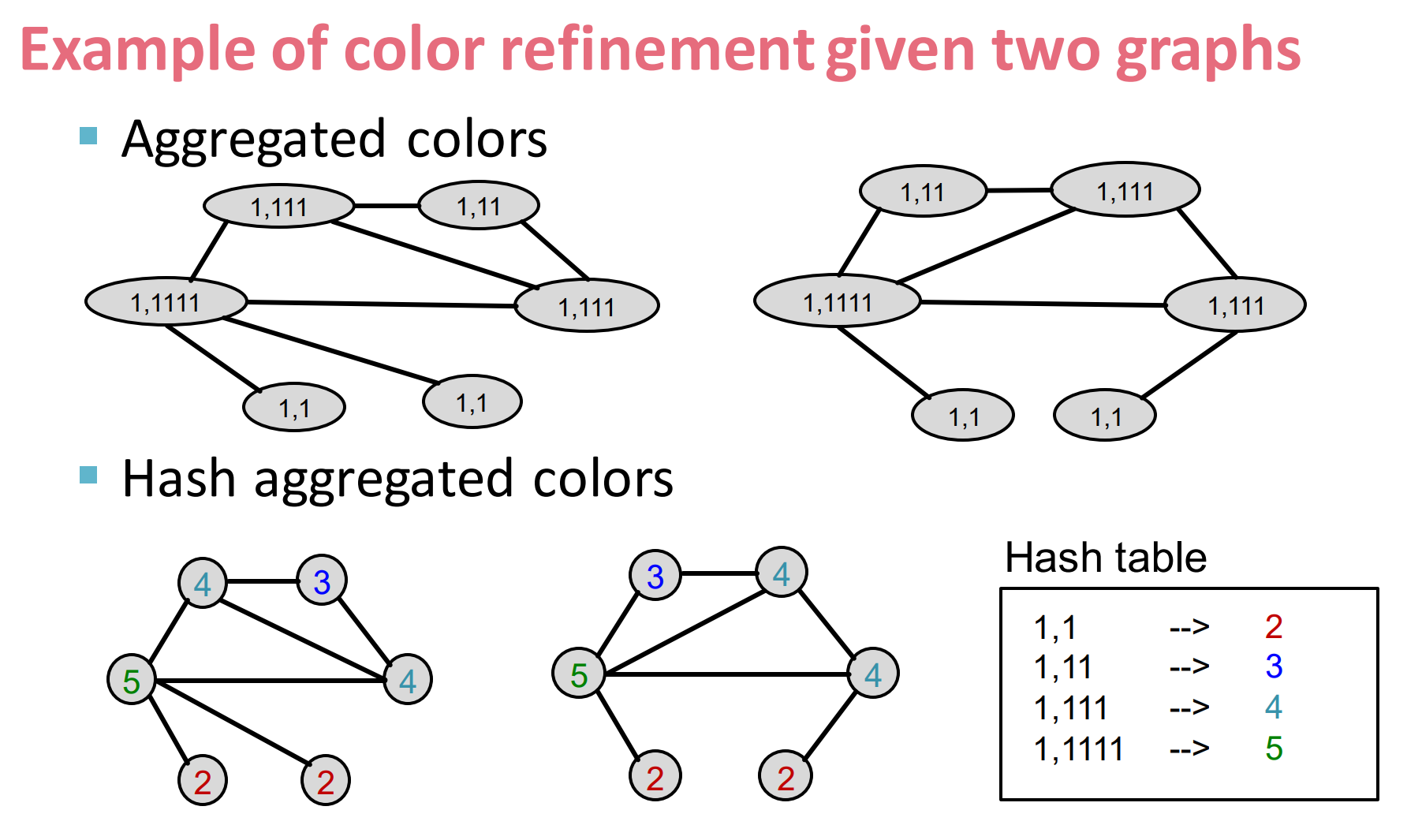
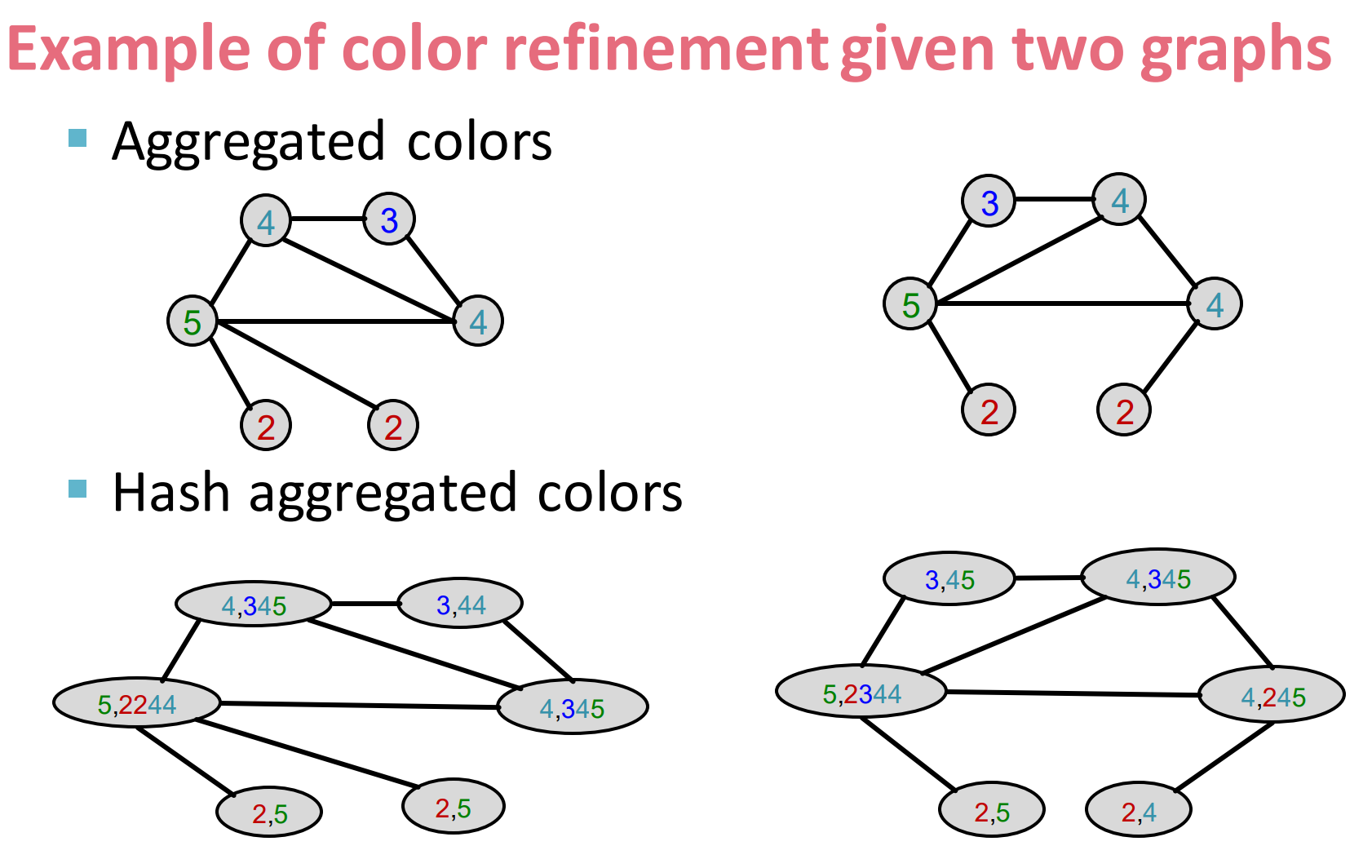
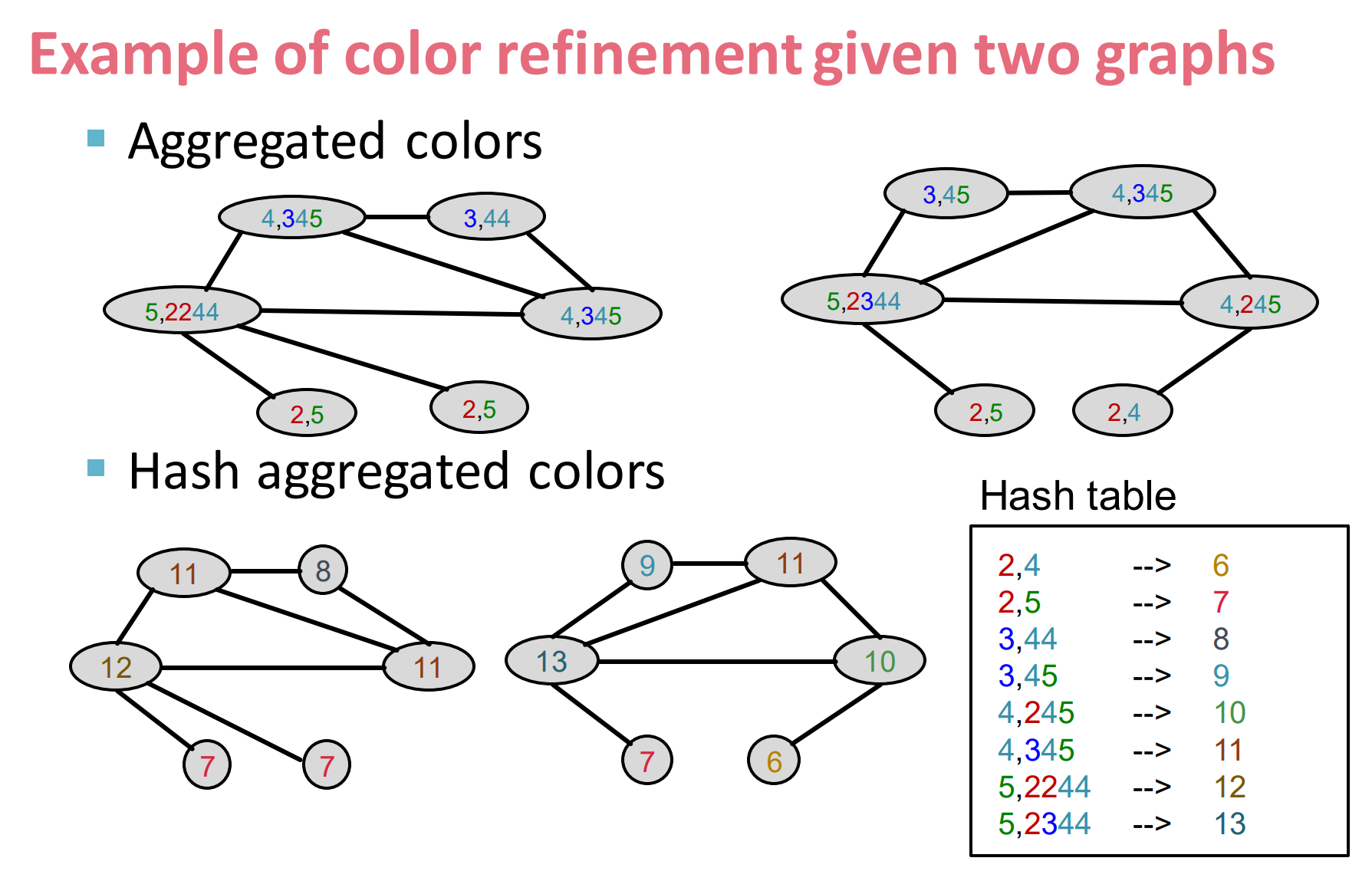
给定两个图来进行color refinement：

先开始对所有节点赋值为1,
aggregate邻居节点信息，具体做法是，第一个G的左上角节点，其有3个为1的的邻居节点，记为(1, 111)。同理有右上角为(1, 11).
按照第一个Hash表赋值，得到聚合后的信息
然后在对其聚合邻居信息, ，第一个G的左上角节点，变成(4, 345)
再按第二个hash表赋值，就行成了最后的节点信息。

经过color refinement 3次后， WL kernel 如上所示。

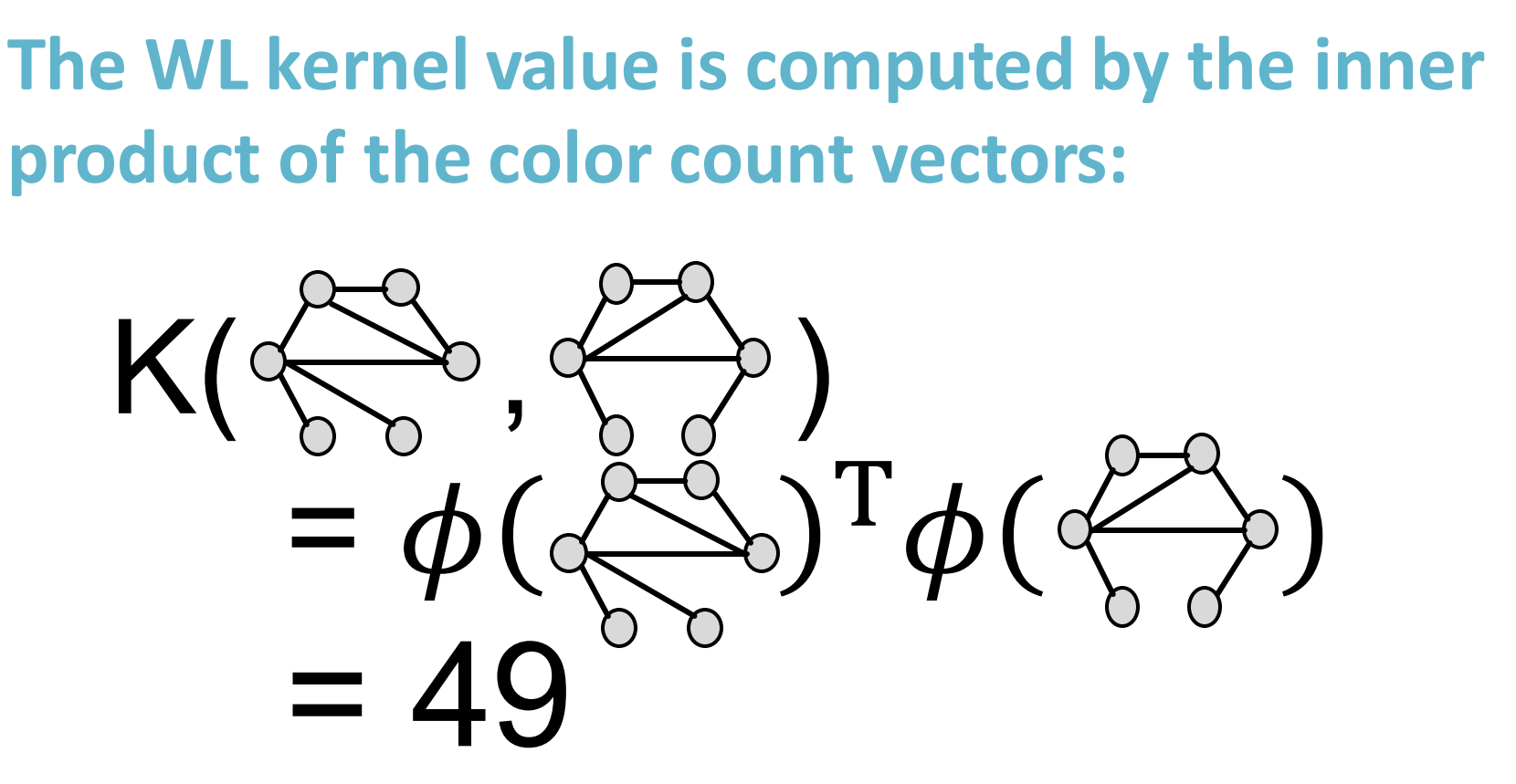
对其进行内积运算后得到36+4+1+4+1+2+1=49.

Weisferiler-Lehman Kernel

WL 核计算高效
- color refinement的时间复杂度每步都是线性的，因为其包含聚合邻居颜色
当计算kernel值时，仅仅只有出现在两个图中的颜色需要记录
- 因此，颜色最多只能是所有节点数目
统计颜色的复杂度跟节点数成线性关系
总之，时间复杂度更变的数目呈线性关系

7. 图级别特征：总结

Inference

[1] cs224w（图机器学习）2021冬季课程学习笔记2

[2] 【CS224W学习笔记 day01】图传统机器学习

[3] 图神经网络的数学基础一: 线性代数和矩阵

[4] 如何简单地理解中心度

[5] Weisfeiler-Lehman Graph Kernels

[6] 传统图机器学习特征提取方法 — 基于链接水平的特征

[7] [A Comparison of Community Clustering Techniques: Fruchterman-Reingold and Wakita-Tsurumi